Electric field
| Electric field | |
|---|---|
Common symbols | E |
meter (V/m) | |
| In SI base units | kg⋅m⋅s−3⋅A−1 |
| Dimension | M L T−3 I−1 |
| Articles about |
| Electromagnetism |
|---|
 |
An electric field (sometimes called E-field
Electric fields are important in many areas of
The electric field is defined as a
Description

The electric field is defined at each point in space as the force that would be experienced by an
The electric field can be visualized with a set of lines whose direction at each point is the same as those of the field, a concept introduced by Michael Faraday,[8] whose term 'lines of force' is still sometimes used. This illustration has the useful property that, when drawn so that each line represents the same amount of flux, the strength of the field is proportional to the density of the lines.[9] Field lines due to stationary charges have several important properties, including that they always originate from positive charges and terminate at negative charges, they enter all good conductors at right angles, and they never cross or close in on themselves.[6]: 479 The field lines are a representative concept; the field actually permeates all the intervening space between the lines. More or fewer lines may be drawn depending on the precision to which it is desired to represent the field.[8] The study of electric fields created by stationary charges is called electrostatics.
Mathematical formulation
Electric fields are caused by
Electrostatics
In the special case of a steady state (stationary charges and currents), the Maxwell-Faraday inductive effect disappears. The resulting two equations (Gauss's law and Faraday's law with no induction term ), taken together, are equivalent to Coulomb's law, which states that a particle with electric charge at position exerts a force on a particle with charge at position of:[13] where
- is the force on charged particle caused by charged particle .
- ε0 is the permittivity of free space.
- is a unit vector directed from to .
- is the displacement vectorfrom to .
Note that must be replaced with , permittivity, when charges are in non-empty media. When the charges and have the same sign this force is positive, directed away from the other charge, indicating the particles repel each other. When the charges have unlike signs the force is negative, indicating the particles attract. To make it easy to calculate the
- is the component of the electric field at due to .
This is the electric field at point due to the point charge ; it is a vector-valued function equal to the Coulomb force per unit charge that a positive point charge would experience at the position . Since this formula gives the electric field magnitude and direction at any point in space (except at the location of the charge itself, , where it becomes infinite) it defines a vector field. From the above formula it can be seen that the electric field due to a point charge is everywhere directed away from the charge if it is positive, and toward the charge if it is negative, and its magnitude decreases with the
The Coulomb force on a charge of magnitude at any point in space is equal to the product of the charge and the electric field at that point The
Superposition principle
Due to the linearity of Maxwell's equations, electric fields satisfy the superposition principle, which states that the total electric field, at a point, due to a collection of charges is equal to the vector sum of the electric fields at that point due to the individual charges.[4] This principle is useful in calculating the field created by multiple point charges. If charges are stationary in space at points , in the absence of currents, the superposition principle says that the resulting field is the sum of fields generated by each particle as described by Coulomb's law: where
- is the unit vector in the direction from point to point
- is the displacement vector from point to point .
Continuous charge distributions
The superposition principle allows for the calculation of the electric field due to a distribution of charge density . By considering the charge in each small volume of space at point as a point charge, the resulting electric field, , at point can be calculated as where
- is the unit vector pointing from to .
- is the displacement vector from to .
The total field is found by summing the contributions from all the increments of volume by integrating the charge density over the volume :
Similar equations follow for a surface charge with
Electric potential
If a system is static, such that magnetic fields are not time-varying, then by Faraday's law, the electric field is curl-free. In this case, one can define an electric potential, that is, a function such that .
In general, however, the electric field cannot be described independently of the magnetic field. Given the magnetic vector potential, A, defined so that , one can still define an electric potential such that: where is the gradient of the electric potential and is the partial derivative of A with respect to time.
Faraday's law of induction can be recovered by taking the curl of that equation [16] which justifies, a posteriori, the previous form for E.
Continuous vs. discrete charge representation
The equations of electromagnetism are best described in a continuous description. However, charges are sometimes best described as discrete points; for example, some models may describe electrons as point sources where charge density is infinite on an infinitesimal section of space.
A charge located at can be described mathematically as a charge density , where the Dirac delta function (in three dimensions) is used. Conversely, a charge distribution can be approximated by many small point charges.
Electrostatic fields
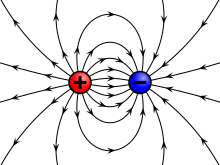
Electrostatic fields are electric fields that do not change with time. Such fields are present when systems of charged matter are stationary, or when electric currents are unchanging. In that case, Coulomb's law fully describes the field.[17]
Parallels between electrostatic and gravitational fields
Coulomb's law, which describes the interaction of electric charges: is similar to Newton's law of universal gravitation: (where ).
This suggests similarities between the electric field E and the gravitational field g, or their associated potentials. Mass is sometimes called "gravitational charge".[18]
Electrostatic and gravitational forces both are central, conservative and obey an inverse-square law.
Uniform fields
A uniform field is one in which the electric field is constant at every point. It can be approximated by placing two conducting plates parallel to each other and maintaining a voltage (potential difference) between them; it is only an approximation because of boundary effects (near the edge of the planes, the electric field is distorted because the plane does not continue). Assuming infinite planes, the magnitude of the electric field E is: where ΔV is the
Electromagnetic fields
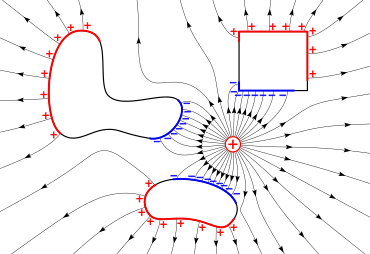
Electromagnetic fields are electric and magnetic fields, which may change with time, for instance when charges are in motion. Moving charges produce a magnetic field in accordance with Ampère's circuital law (with Maxwell's addition), which, along with Maxwell's other equations, defines the magnetic field, , in terms of its curl: where is the current density, is the vacuum permeability, and is the vacuum permittivity.
Both the
Energy in the electric field
The total energy per unit volume stored by the electromagnetic field is[19] where ε is the permittivity of the medium in which the field exists, its
As E and B fields are coupled, it would be misleading to split this expression into "electric" and "magnetic" contributions. In particular, an electrostatic field in any given frame of reference in general transforms into a field with a magnetic component in a relatively moving frame. Accordingly, decomposing the electromagnetic field into an electric and magnetic component is frame-specific, and similarly for the associated energy.
The total energy UEM stored in the electromagnetic field in a given volume V is
Electric displacement field
Definitive equation of vector fields
In the presence of matter, it is helpful to extend the notion of the electric field into three vector fields:[20] where P is the
Constitutive relation
The E and D fields are related by the permittivity of the material, ε.[21][20]
For linear, homogeneous, isotropic materials E and D are proportional and constant throughout the region, there is no position dependence:
For inhomogeneous materials, there is a position dependence throughout the material:[22]
For anisotropic materials the E and D fields are not parallel, and so E and D are related by the permittivity tensor (a 2nd order tensor field), in component form:
For non-linear media, E and D are not proportional. Materials can have varying extents of linearity, homogeneity and isotropy.
Relativistic effects on electric field
Point charge in uniform motion
The invariance of the form of Maxwell's equations under Lorentz transformation can be used to derive the electric field of a uniformly moving point charge. The charge of a particle is considered frame invariant, as supported by experimental evidence.[23] Alternatively the electric field of uniformly moving point charges can be derived from the Lorentz transformation of four-force experienced by test charges in the source's rest frame given by Coulomb's law and assigning electric field and magnetic field by their definition given by the form of Lorentz force.[24] However the following equation is only applicable when no acceleration is involved in the particle's history where Coulomb's law can be considered or symmetry arguments can be used for solving Maxwell's equations in a simple manner. The electric field of such a uniformly moving point charge is hence given by:[25] where is the charge of the point source, is the position vector from the point source to the point in space, is the ratio of observed speed of the charge particle to the speed of light and is the angle between and the observed velocity of the charged particle.
The above equation reduces to that given by Coulomb's law for non-relativistic speeds of the point charge. Spherical symmetry is not satisfied due to breaking of symmetry in the problem by specification of direction of velocity for calculation of field. To illustrate this, field lines of moving charges are sometimes represented as unequally spaced radial lines which would appear equally spaced in a co-moving reference frame.[23]
Propagation of disturbances in electric fields
Special theory of relativity imposes the principle of locality, that requires cause and effect to be time-like separated events where the causal efficacy does not travel faster than the speed of light.[26] Maxwell's laws are found to confirm to this view since the general solutions of fields are given in terms of retarded time which indicate that electromagnetic disturbances travel at the speed of light. Advanced time, which also provides a solution for Maxwell's law are ignored as an unphysical solution.

For the motion of a charged particle, considering for example the case of a moving particle with the above described electric field coming to an abrupt stop, the electric fields at points far from it do not immediately revert to that classically given for a stationary charge. On stopping, the field around the stationary points begin to revert to the expected state and this effect propagates outwards at the speed of light while the electric field lines far away from this will continue to point radially towards an assumed moving charge. This virtual particle will never be outside the range of propagation of the disturbance in electromagnetic field, since charged particles are restricted to have speeds slower than that of light, which makes it impossible to construct a Gaussian surface in this region that violates Gauss's law. Another technical difficulty that supports this is that charged particles travelling faster than or equal to speed of light no longer have a unique retarded time. Since electric field lines are continuous, an electromagnetic pulse of radiation is generated that connects at the boundary of this disturbance travelling outwards at the speed of light.[27] In general, any accelerating point charge radiates electromagnetic waves however, non-radiating acceleration is possible in a systems of charges.
Arbitrarily moving point charge
For arbitrarily moving point charges, propagation of potential fields such as Lorenz gauge fields at the speed of light needs to be accounted for by using Liénard–Wiechert potential.[28] Since the potentials satisfy Maxwell's equations, the fields derived for point charge also satisfy Maxwell's equations. The electric field is expressed as:[29] where is the charge of the point source, is retarded time or the time at which the source's contribution of the electric field originated, is the position vector of the particle, is a unit vector pointing from charged particle to the point in space, is the velocity of the particle divided by the speed of light, and is the corresponding Lorentz factor. The retarded time is given as solution of:
The uniqueness of solution for for given , and is valid for charged particles moving slower than speed of light. Electromagnetic radiation of accelerating charges is known to be caused by the acceleration dependent term in the electric field from which relativistic correction for Larmor formula is obtained.[29]
There exist yet another set of solutions for Maxwell's equation of the same form but for advanced time instead of retarded time given as a solution of:
Since the physical interpretation of this indicates that the electric field at a point is governed by the particle's state at a point of time in the future, it is considered as an unphysical solution and hence neglected. However, there have been theories exploring the advanced time solutions of Maxwell's equations, such as Feynman Wheeler absorber theory.
The above equation, although consistent with that of uniformly moving point charges as well as its non-relativistic limit, are not corrected for quantum-mechanical effects.
Common formulæ
Electric field infinitely close to a conducting surface in electrostatic equilibrium having charge density at that point is since charges are only formed on the surface and the surface at the infinitesimal scale resembles an infinite 2D plane. In the absence of external fields, spherical conductors exhibit a uniform charge distribution on the surface and hence have the same electric field as that of uniform spherical surface distribution.
See also
- Classical electromagnetism
- Relativistic electromagnetism
- Electricity
- History of electromagnetic theory
- Electromagnetic field
- Magnetism
- Teltron tube
- Teledeltos, a conductive paper that may be used as a simple analog computer for modelling fields
References
- S2CID 125014664.
- ISBN 978-0-201-02115-8.
- ISBN 978-1-107-01402-2.
- ^ ISBN 978-1305142824.
- ISBN 978-92-822-2272-0, p. 23
- ^ ISBN 0-201-07199-1
- ISBN 9971-5-0921-0
- ^ ISBN 0-582-42629-4
- ISBN 9780470978467.
- ^ OCLC 40251748.
- ^ Purcell, p. 25: "Gauss's Law: the flux of the electric field E through any closed surface ... equals 1/e times the total charge enclosed by the surface."
- ^ Purcell, p 356: "Faraday's Law of Induction."
- ^ Purcell, p7: "... the interaction between electric charges at rest is described by Coulomb's Law: two stationary electric charges repel or attract each other with a force proportional to the product of the magnitude of the charges and inversely proportional to the square of the distance between them.
- ISBN 978-1139503556.
- ^ gwrowe (8 October 2011). "Curl & Potential in Electrostatics" (PDF). physicspages.com. Archived from the original (PDF) on 22 March 2019. Retrieved 2 November 2020.
- ]
- ^ Purcell, pp. 5–7.
- ^ Salam, Abdus (16 December 1976). "Quarks and leptons come out to play". New Scientist. 72: 652.[permanent dead link]
- ISBN 9781108420419.
- ^ ISBN 978-0-471-92712-9.
- ISBN 0-7131-2459-8.
- ISBN 978-0-7581-6499-5.
In Maxwell's equations… ε is a function of the co-ordinates.
- ^ )
- ISBN 978-1-4899-6258-4.
- ^ Heaviside, Oliver. Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge.
- OCLC 804823303.
- OCLC 1105718330.)
{{cite book}}: CS1 maint: location missing publisher (link - OCLC 1021068059.
- ^ OCLC 38073290.
- Purcell, Edward; Morin, David (2013). Electricity and Magnetism (3rd ed.). Cambridge University Press, New York. ISBN 978-1-107-01402-2.
- Browne, Michael (2011). Physics for Engineering and Science (2nd ed.). McGraw-Hill, Schaum, New York. ISBN 978-0-07-161399-6.
External links
- Electric field in "Electricity and Magnetism", R Nave – Hyperphysics, Georgia State University
- Frank Wolfs's lectures at University of Rochester, chapters 23 and 24
- Fields Archived 2010-05-27 at the Wayback Machine – a chapter from an online textbook


















































































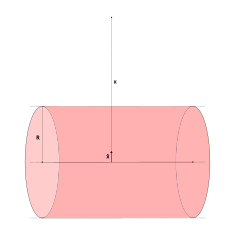









![{\displaystyle \mathbf {E} ={\frac {\sigma }{2\varepsilon _{0}}}\left[1-{\frac {x}{\sqrt {x^{2}+R^{2}}}}\right]{\hat {\mathbf {x} }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6846763e54d7afcc4b7823929fd0a8993d9dbf49)






