Cellular automaton: Difference between revisions
→Rule space: added number of possible rules for 2D CA |
→Generative art and music: added extra example Tag: Reverted |
||
| Line 180: | Line 180: | ||
===Generative art and music=== |
===Generative art and music=== |
||
Cellular automata have been used in [[generative music]]<ref>Burraston, Dave, and Ernest Edmonds. "[https://web2.qatar.cmu.edu/~gdicaro/15382-Spring18/additional/generative-music-ca-review.pdf Cellular automata in generative electronic music and sonic art: a historical and technical review]." Digital Creativity 16.3 (2005): 165-185.</ref> and [[evolutionary music]] composition<ref>Miranda, Eduardo Reck. "[https://sites.google.com/site/jimmycifuentes/EvolvingCAMusic.pdf Evolving cellular automata music: From sound synthesis to composition]." Proceedings of 2001 Workshop on Artificial Life Models for Musical Applications. 2001.</ref> and [[procedural terrain]] generation in video games.<ref>Miranda, Eduardo Reck. "[https://sites.google.com/site/jimmycifuentes/EvolvingCAMusic.pdf Evolving cellular automata music: From sound synthesis to composition]." Proceedings of 2001 Workshop on Artificial Life Models for Musical Applications. 2001.</ref> |
Cellular automata have been used in [[generative music]]<ref>Burraston, Dave, and Ernest Edmonds. "[https://web2.qatar.cmu.edu/~gdicaro/15382-Spring18/additional/generative-music-ca-review.pdf Cellular automata in generative electronic music and sonic art: a historical and technical review]." Digital Creativity 16.3 (2005): 165-185.</ref> (see: [http://tones.wolfram.com/ WolframTones]) and [[evolutionary music]] composition<ref>Miranda, Eduardo Reck. "[https://sites.google.com/site/jimmycifuentes/EvolvingCAMusic.pdf Evolving cellular automata music: From sound synthesis to composition]." Proceedings of 2001 Workshop on Artificial Life Models for Musical Applications. 2001.</ref> and [[procedural terrain]] generation in video games.<ref>Miranda, Eduardo Reck. "[https://sites.google.com/site/jimmycifuentes/EvolvingCAMusic.pdf Evolving cellular automata music: From sound synthesis to composition]." Proceedings of 2001 Workshop on Artificial Life Models for Musical Applications. 2001.</ref> |
||
==Specific rules== |
==Specific rules== |
||
Revision as of 22:46, 8 March 2021
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete
A cellular automaton consists of a regular grid of cells, each in one of a finite number of states, such as on and off (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its neighborhood is defined relative to the specified cell. An initial state (time t = 0) is selected by assigning a state for each cell. A new generation is created (advancing t by 1), according to some fixed rule (generally, a mathematical function)[3] that determines the new state of each cell in terms of the current state of the cell and the states of the cells in its neighborhood. Typically, the rule for updating the state of cells is the same for each cell and does not change over time, and is applied to the whole grid simultaneously,[4] though exceptions are known, such as the stochastic cellular automaton and asynchronous cellular automaton.
The concept was originally discovered in the 1940s by
The primary classifications of cellular automata, as outlined by Wolfram, are numbered one to four. They are, in order, automata in which patterns generally stabilize into
Overview
One way to simulate a two-dimensional cellular automaton is with an infinite sheet of
It is usually assumed that every cell in the universe starts in the same state, except for a finite number of cells in other states; the assignment of state values is called a configuration.[7] More generally, it is sometimes assumed that the universe starts out covered with a periodic pattern, and only a finite number of cells violate that pattern. The latter assumption is common in one-dimensional cellular automata.

Cellular automata are often simulated on a finite grid rather than an infinite one. In two dimensions, the universe would be a rectangle instead of an infinite plane. The obvious problem with finite grids is how to handle the cells on the edges. How they are handled will affect the values of all the cells in the grid. One possible method is to allow the values in those cells to remain constant. Another method is to define neighborhoods differently for these cells. One could say that they have fewer neighbors, but then one would also have to define new rules for the cells located on the edges. These cells are usually handled with a toroidal arrangement: when one goes off the top, one comes in at the corresponding position on the bottom, and when one goes off the left, one comes in on the right. (This essentially simulates an infinite periodic tiling, and in the field of
History

Ulam and von Neumann created a method for calculating liquid motion in the late 1950s. The driving concept of the method was to consider a liquid as a group of discrete units and calculate the motion of each based on its neighbors' behaviors.
Also in the 1940s,
By the end of the 1950s it had been noted that cellular automata could be viewed as
In the 1960s, cellular automata were studied as a particular type of
In 1969, German computer pioneer Konrad Zuse published his book Calculating Space, proposing that the physical laws of the universe are discrete by nature, and that the entire universe is the output of a deterministic computation on a single cellular automaton; "Zuse's Theory" became the foundation of the field of study called digital physics.[22]
Also in 1969 computer scientist Alvy Ray Smith completed a Stanford PhD dissertation on Cellular Automata Theory, the first mathematical treatment of CA as a general class of computers. Many papers came from this dissertation: He showed the equivalence of neighborhoods of various shapes, how to reduce a Moore to a von Neumann neighborhood or how to reduce any neighborhood to a von Neumann neighborhood.[23] He proved that two-dimensional CA are computation universal, introduced 1-dimensional CA, and showed that they too are computation universal, even with simple neighborhoods.[24] He showed how to subsume the complex von Neumann proof of construction universality (and hence self-reproducing machines) into a consequence of computation universality in a 1-dimensional CA.[25] Intended as the introduction to the German edition of von Neumann's book on CA, he wrote a survey of the field with dozens of references to papers, by many authors in many countries over a decade or so of work, often overlooked by modern CA researchers.[26]
In the 1970s a two-state, two-dimensional cellular automaton named Game of Life became widely known, particularly among the early computing community. Invented by John Conway and popularized by Martin Gardner in a Scientific American article,[27] its rules are as follows:
- Any live cell with fewer than two live neighbours dies, as if caused by underpopulation.
- Any live cell with two or three live neighbours lives on to the next generation.
- Any live cell with more than three live neighbours dies, as if by overpopulation.
- Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.
Despite its simplicity, the system achieves an impressive diversity of behavior, fluctuating between apparent randomness and order. One of the most apparent features of the Game of Life is the frequent occurrence of gliders, arrangements of cells that essentially move themselves across the grid. It is possible to arrange the automaton so that the gliders interact to perform computations, and after much effort it has been shown that the Game of Life can emulate a universal Turing machine.[28] It was viewed as a largely recreational topic, and little follow-up work was done outside of investigating the particularities of the Game of Life and a few related rules in the early 1970s.[29]
In 2002 Wolfram published a 1280-page text A New Kind of Science, which extensively argues that the discoveries about cellular automata are not isolated facts but are robust and have significance for all disciplines of science.[33] Despite confusion in the press,[34][35] the book did not argue for a fundamental theory of physics based on cellular automata,[36] and although it did describe a few specific physical models based on cellular automata,[37] it also provided models based on qualitatively different abstract systems.[38]
Classification
Wolfram, in A New Kind of Science and several papers dating from the mid-1980s, defined four classes into which cellular automata and several other simple computational models can be divided depending on their behavior. While earlier studies in cellular automata tended to try to identify type of patterns for specific rules, Wolfram's classification was the first attempt to classify the rules themselves. In order of complexity the classes are:
- Class 1: Nearly all initial patterns evolve quickly into a stable, homogeneous state. Any randomness in the initial pattern disappears.[39]
- Class 2: Nearly all initial patterns evolve quickly into stable or oscillating structures. Some of the randomness in the initial pattern may filter out, but some remains. Local changes to the initial pattern tend to remain local.[39]
- Class 3: Nearly all initial patterns evolve in a pseudo-random or chaotic manner. Any stable structures that appear are quickly destroyed by the surrounding noise. Local changes to the initial pattern tend to spread indefinitely.[39]
- Class 4: Nearly all initial patterns evolve into structures that interact in complex and interesting ways, with the formation of local structures that are able to survive for long periods of time.[40] Class 2 type stable or oscillating structures may be the eventual outcome, but the number of steps required to reach this state may be very large, even when the initial pattern is relatively simple. Local changes to the initial pattern may spread indefinitely. Wolfram has conjectured that many class 4 cellular automata, if not all, are capable of universal computation. This has been proven for Rule 110 and Conway's Game of Life.
These definitions are qualitative in nature and there is some room for interpretation. According to Wolfram, "...with almost any general classification scheme there are inevitably cases which get assigned to one class by one definition and another class by another definition. And so it is with cellular automata: there are occasionally rules...that show some features of one class and some of another."[41] Wolfram's classification has been empirically matched to a clustering of the compressed lengths of the outputs of cellular automata.[42]
There have been several attempts to classify cellular automata in formally rigorous classes, inspired by the Wolfram's classification. For instance, Culik and Yu proposed three well-defined classes (and a fourth one for the automata not matching any of these), which are sometimes called Culik-Yu classes; membership in these proved undecidable.[43][44][45] Wolfram's class 2 can be partitioned into two subgroups of stable (fixed-point) and oscillating (periodic) rules.[46]
The idea that there are 4 classes of dynamical system came originally from nobel-prize winning chemist Ilya Prigogine who identified these 4 classes of thermodynamical systems - (1) systems in thermodynamic equilibrium, (2) spatially/temporally uniform systems, (3) chaotic systems, and (4) complex far-from-equilibrium systems with dissipative structures (see figure 1 in Nicolis' paper (Prigogine's student)).[47]
Reversible
A cellular automaton is reversible if, for every current configuration of the cellular automaton, there is exactly one past configuration (
For one-dimensional cellular automata there are known algorithms for deciding whether a rule is reversible or irreversible.[52][53] However, for cellular automata of two or more dimensions reversibility is undecidable; that is, there is no algorithm that takes as input an automaton rule and is guaranteed to determine correctly whether the automaton is reversible. The proof by Jarkko Kari is related to the tiling problem by Wang tiles.[54]
Reversible cellular automata are often used to simulate such physical phenomena as gas and fluid dynamics, since they obey the laws of thermodynamics. Such cellular automata have rules specially constructed to be reversible. Such systems have been studied by Tommaso Toffoli, Norman Margolus and others. Several techniques can be used to explicitly construct reversible cellular automata with known inverses. Two common ones are the second-order cellular automaton and the block cellular automaton, both of which involve modifying the definition of a cellular automaton in some way. Although such automata do not strictly satisfy the definition given above, it can be shown that they can be emulated by conventional cellular automata with sufficiently large neighborhoods and numbers of states, and can therefore be considered a subset of conventional cellular automata. Conversely, it has been shown that every reversible cellular automaton can be emulated by a block cellular automaton.[55][56]
Totalistic
A special class of cellular automata are totalistic cellular automata. The state of each cell in a totalistic cellular automaton is represented by a number (usually an integer value drawn from a finite set), and the value of a cell at time t depends only on the sum of the values of the cells in its neighborhood (possibly including the cell itself) at time t − 1.[57][58] If the state of the cell at time t depends on both its own state and the total of its neighbors at time t − 1 then the cellular automaton is properly called outer totalistic.[58] Conway's Game of Life is an example of an outer totalistic cellular automaton with cell values 0 and 1; outer totalistic cellular automata with the same Moore neighborhood structure as Life are sometimes called life-like cellular automata.[59][60]
Related automata
There are many possible generalizations of the cellular automaton concept.

One way is by using something other than a rectangular (cubic, etc.) grid. For example, if a plane is
Also, rules can be probabilistic rather than deterministic. Such cellular automata are called
The neighborhood or rules could change over time or space. For example, initially the new state of a cell could be determined by the horizontally adjacent cells, but for the next generation the vertical cells would be used.
In cellular automata, the new state of a cell is not affected by the new state of other cells. This could be changed so that, for instance, a 2 by 2 block of cells can be determined by itself and the cells adjacent to itself.
There are continuous automata. These are like totalistic cellular automata, but instead of the rule and states being discrete (e.g. a table, using states {0,1,2}), continuous functions are used, and the states become continuous (usually values in [0,1]). The state of a location is a finite number of real numbers. Certain cellular automata can yield diffusion in liquid patterns in this way.
There are known examples of continuous spatial automata, which exhibit propagating phenomena analogous to gliders in the Game of Life.[63]
Graph rewriting automata are extensions of cellular automata based on
Combinations automata function by checking if an odd/even indexed pair is equal to permutation X. If so, return X of the rulestring (for example: "120012101"). These CA work with brickwall neighborhoods. These CA types also act like Logic gate(s). For instance, the equivalent of the XOR gate in Combinations produces a Sierpiński triangle when the initial state is a single centered cell.
Elementary cellular automata
The simplest nontrivial cellular automaton would be one-dimensional, with two possible states per cell, and a cell's neighbors defined as the adjacent cells on either side of it. A cell and its two neighbors form a neighborhood of 3 cells, so there are 23 = 8 possible patterns for a neighborhood. A rule consists of deciding, for each pattern, whether the cell will be a 1 or a 0 in the next generation. There are then 28 = 256 possible rules.[6]
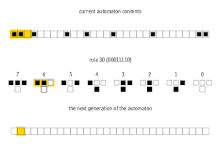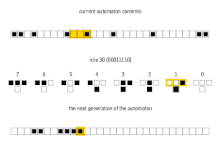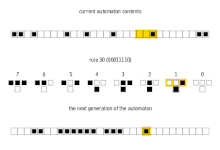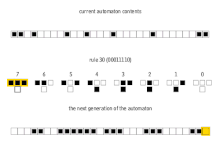
These 256 cellular automata are generally referred to by their Wolfram code, a standard naming convention invented by Wolfram that gives each rule a number from 0 to 255. A number of papers have analyzed and compared these 256 cellular automata. The rule 30 and rule 110 cellular automata are particularly interesting. The images below show the history of each when the starting configuration consists of a 1 (at the top of each image) surrounded by 0s. Each row of pixels represents a generation in the history of the automaton, with t=0 being the top row. Each pixel is colored white for 0 and black for 1.

Rule 30 cellular automaton
| current pattern | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| new state for center cell | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Rule 30 exhibits class 3 behavior, meaning even simple input patterns such as that shown lead to chaotic, seemingly random histories.

Rule 110 cellular automaton
| current pattern | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| new state for center cell | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Rule 110, like the Game of Life, exhibits what Wolfram calls class 4 behavior, which is neither completely random nor completely repetitive. Localized structures appear and interact in various complicated-looking ways. In the course of the development of
Rule space

An elementary cellular automaton rule is specified by 8 bits, and all elementary cellular automaton rules can be considered to sit on the vertices of the 8-dimensional unit hypercube. This unit hypercube is the cellular automaton rule space. For next-nearest-neighbor cellular automata, a rule is specified by 25 = 32 bits, and the cellular automaton rule space is a 32-dimensional unit hypercube. A distance between two rules can be defined by the number of steps required to move from one vertex, which represents the first rule, and another vertex, representing another rule, along the edge of the hypercube. This rule-to-rule distance is also called the Hamming distance.
Cellular automaton rule space allows us to ask the question concerning whether rules with similar dynamical behavior are "close" to each other. Graphically drawing a high dimensional hypercube on the 2-dimensional plane remains a difficult task, and one crude locator of a rule in the hypercube is the number of bit-1 in the 8-bit string for elementary rules (or 32-bit string for the next-nearest-neighbor rules). Drawing the rules in different Wolfram classes in these slices of the rule space show that class 1 rules tend to have lower number of bit-1s, thus located in one region of the space, whereas class 3 rules tend to have higher proportion (50%) of bit-1s.[46]
For larger cellular automaton rule space, it is shown that class 4 rules are located between the class 1 and class 3 rules.[67] This observation is the foundation for the phrase edge of chaos, and is reminiscent of the phase transition in thermodynamics.
Applications
Biology

Some biological processes occur—or can be simulated—by cellular automata.
Patterns of some seashells, like the ones in the genera Conus and Cymbiola, are generated by natural cellular automata. The pigment cells reside in a narrow band along the shell's lip. Each cell secretes pigments according to the activating and inhibiting activity of its neighbor pigment cells, obeying a natural version of a mathematical rule.[68] The cell band leaves the colored pattern on the shell as it grows slowly. For example, the widespread species Conus textile bears a pattern resembling Wolfram's rule 30 cellular automaton.[68]
Plants regulate their intake and loss of gases via a cellular automaton mechanism. Each
Moving wave patterns on the skin of cephalopods can be simulated with a two-state, two-dimensional cellular automata, each state corresponding to either an expanded or retracted chromatophore.[70]
Threshold automata have been invented to simulate neurons, and complex behaviors such as recognition and learning can be simulated.[71]
Fibroblasts bear similarities to cellular automata, as each fibroblast only interacts with its neighbors.[72]
Chemistry
The
Physics

Probabilistic cellular automata are used in
Computer science, coding, and communication
Cellular automaton processors are physical implementations of CA concepts, which can process information computationally. Processing elements are arranged in a regular grid of identical cells. The grid is usually a square tiling, or
Rule 30 was originally suggested as a possible block cipher for use in cryptography. Two-dimensional cellular automata can be used for constructing a pseudorandom number generator.[79]
Cellular automata have been proposed for public-key cryptography. The one-way function is the evolution of a finite CA whose inverse is believed to be hard to find. Given the rule, anyone can easily calculate future states, but it appears to be very difficult to calculate previous states.
CA have been applied to design error correction codes in a paper by D. Roy Chowdhury, S. Basu, I. Sen Gupta, and P. Pal Chaudhuri. The paper defines a new scheme of building single bit error correction and double bit error detection (SEC-DED) codes using CA, and also reports a fast hardware decoder for the code.[80]
Other problems that can be solved with cellular automata include:
- Firing squad synchronization problem
- Majority problem
Generative art and music
Cellular automata have been used in
Specific rules
Specific types of cellular automata include:
- Brian's Brain
- Codd's cellular automaton
- CoDi
- Langton's ant
- Langton's loops
- Nobili cellular automata
- Rule 90
- Rule 184
- von Neumann cellular automata
- Wireworld
See also
- Agent-based model – Type of computational models
- Automata theory – Study of abstract machines and automata
- Bidirectional traffic – Two streams of traffic that flow in opposite directions
- Cyclic cellular automaton
- Excitable medium – Nonlinear dynamical system
- Golly
- Movable cellular automaton – Method in computational solid mechanics based on the discrete concept
- Quantum cellular automaton – Abstract model of quantum computation
- Spatial decision support system – Computerised aid to land use decisions
- Turmite – Turing machine on a two-dimensional grid
- Category:Cellular automata in popular culture
- Discrete calculus
Notes
- ISBN 0-14-016734-X
- ^ .
- ISBN 9780262200608.
- ISBN 9781118030639.
- ^ a b c d Kier, Seybold, Cheng 2005, p. 15
- ^ a b Bialynicki-Birula, Bialynicka-Birula 2004, p. 9
- ^ Schiff 2011, p. 41
- ISBN 978-1402757969.
- ^ a b Schiff 2011, p. 1
- ^ John von Neumann, "The general and logical theory of automata," in L.A. Jeffress, ed., Cerebral Mechanisms in Behavior – The Hixon Symposium, John Wiley & Sons, New York, 1951, pp. 1–31.
- .; Sci. Am. 1955; 192:6 (errata).
- ^ Schiff 2011, p. 3
- ^ Ilachinski 2001, p. xxix
- ^ Bialynicki-Birula, Bialynicka-Birula 2004, p. 8
- ^ a b Wolfram 2002, p. 876
- ^ von Neumann, John; Burks, Arthur W. (1966). Theory of Self-Reproducing Automata. University of Illinois Press.
- ^ PMID 20245817.
- S2CID 121306408.
- S2CID 4348759.
- ISBN 978-1-57955-008-0.
- S2CID 21803927.
- ^ Schiff 2011, p. 182
- ^ Smith, Alvy Ray. "Cellular Automata Complexity Trade-Offs" (PDF).
- ^ Smith, Alvy Ray. "Simple Computation-Universal Cellular Spaces" (PDF).
- ^ Smith, Alvy Ray. "Simple Nontrivial Self-Reproducing Machines" (PDF).
- ^ Smith, Alvy Ray. "Introduction to and Survey of Cellular Automata or Polyautomata Theory" (PDF).
- .
- ^ Paul Chapman. Life universal computer. http://www.igblan.free-online.co.uk/igblan/ca/ November 2002
- ^ Wainwright 2010, p. 16
- ^ a b c d e Wolfram 2002, p. 880
- ^ Wolfram 2002, p. 881
- S2CID 122484855.
- ^ Wolfram 2002, pp. 1–7
- ^ Johnson, George (9 June 2002). "'A New Kind of Science': You Know That Space-Time Thing? Never Mind". The New York Times. The New York Times Company. Retrieved 22 January 2013.
- ^ "The Science of Everything". The Economist. 30 May 2002. Retrieved 22 January 2013.
- ^ Wolfram 2002, pp. 433–546
- ^ Wolfram 2002, pp. 51–114
- ^ Wolfram 2002, pp. 115–168
- ^ a b c Ilachinsky 2001, p. 12
- ^ Ilachinsky 2001, p. 13
- ^ Wolfram 2002, p. 231
- S2CID 15364755.
- ISBN 978-0-7923-5493-2.
- ISBN 978-981-02-2221-5.
- ISBN 978-3-540-56149-1.
- ^ a b Li, Wentian; Packard, Norman (1990). "The structure of the elementary cellular automata rule space" (PDF). Complex Systems. 4: 281–297. Retrieved 25 January 2013.
- PMID 16592170. Retrieved 25 March 2017.
- ^ a b Kari, Jarrko 1991, p. 379
- .
- ISBN 978-2-84703-033-4.
- ^ Schiff 2011, p. 103
- .
- ^ Sutner, Klaus (1991). "De Bruijn Graphs and Linear Cellular Automata" (PDF). Complex Systems. 5: 19–30.
- .
- .
- ^ Durand-Lose, Jérôme (2001). "Representing reversible cellular automata with reversible block cellular automata". Discrete Mathematics and Theoretical Computer Science. AA: 145–154. Archived from the original on 15 May 2011.
- ^ Wolfram 2002, p. 60
- ^ ISBN 978-981-238-183-5.
- .
- ^ Eppstein 2010, pp. 72–73
- ^ Jacob Aron. "First gliders navigate ever-changing Penrose universe". New Scientist.
- ^ Murray, J. "Mathematical Biology II". Springer.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Pivato, M: "RealLife: The continuum limit of Larger than Life cellular automata", Theoretical Computer Science, 372 (1), March 2007, pp. 46–68
- ISBN 978-3-642-01283-9.
- S2CID 10636328.
- ^ Weinberg, Steven (24 October 2002). "Is the Universe a Computer?". The New York Review of Books. Retrieved 12 October 2012.
- .
- ^ a b c Coombs, Stephen (15 February 2009), The Geometry and Pigmentation of Seashells (PDF), pp. 3–4, archived from the original (PDF) on 7 January 2013, retrieved 2 September 2012
- PMID 14732685.
- ^ "Archived copy" (PDF). Archived from the original (PDF) on 4 March 2016. Retrieved 14 September 2008.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Ilachinsky 2001, p. 275
- ^ Yves Bouligand (1986). Disordered Systems and Biological Organization. pp. 374–375.
- ^ A. K. Dewdney, The hodgepodge machine makes waves, Scientific American, p. 104, August 1988.
- .
- OCLC 845714772.
- OCLC 920137477.
- doi:10.4249/scholarpedia.10314.)
{{cite journal}}: CS1 maint: unflagged free DOI (link - ^ Muhtaroglu, Ali (August 1996). "4.1 Cellular Automaton Processor (CAP)". Cellular Automaton Processor Based Systems for Genetic Sequence Comparison/Database Searching. Cornell University. pp. 62–74.
- .
- .
- ^ Burraston, Dave, and Ernest Edmonds. "Cellular automata in generative electronic music and sonic art: a historical and technical review." Digital Creativity 16.3 (2005): 165-185.
- ^ Miranda, Eduardo Reck. "Evolving cellular automata music: From sound synthesis to composition." Proceedings of 2001 Workshop on Artificial Life Models for Musical Applications. 2001.
- ^ Miranda, Eduardo Reck. "Evolving cellular automata music: From sound synthesis to composition." Proceedings of 2001 Workshop on Artificial Life Models for Musical Applications. 2001.
References
- ISBN 978-1-84996-216-2.
- Bialynicki-Birula, Iwo; Bialynicka-Birula, Iwona (2004). Modeling Reality: How Computers Mirror Life. ISBN 978-0198531005.
- Chopard, Bastien; Droz, Michel (2005). Cellular Automata Modeling of Physical Systems. ISBN 978-0-521-46168-9.
- Gutowitz, Howard, ed. (1991). Cellular Automata: Theory and Experiment. ISBN 9780262570862.
- Ilachinski, Andrew (2001). Cellular Automata: A Discrete Universe. ISBN 9789812381835.
- Kier, Lemont B.; Seybold, Paul G.; Cheng, Chao-Kun (2005). Modeling Chemical Systems using Cellular Automata. Springer. ISBN 9781402036576.
- Kroc, Jiří; Jiménez-Morales, Francisco; Guisado, José Luis; Lemos, María Carmen; Tkáč, Jakub (December 2019). "Building Efficient Computational Cellular Automata Models of Complex Systems: Background, Applications, Results, Software, and Pathologies". Advances in Complex Systems. 22 (5): 1950013 (38 pages). .
- ISBN 978-1579550080.
- Cellular automaton FAQ from the newsgroup comp.theory.cell-automata
- "Neighbourhood Survey" (includes discussion on triangular grids, and larger neighborhood CAs)
- von Neumann, John, 1966, The Theory of Self-reproducing Automata, A. Burks, ed., Univ. of Illinois Press, Urbana, IL.
- Cosma Shalizi's Cellular Automata Notebook contains an extensive list of academic and professional reference material.
- Wolfram's papers on CAs
- A.M. Turing. 1952. The Chemical Basis of Morphogenesis. Phil. Trans. Royal Society, vol. B237, pp. 37–72. (proposes reaction-diffusion, a type of continuous automaton).
- Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)
- The Evolutionary Design of Collective Computation in Cellular Automata, James P. Crutchfeld, Melanie Mitchell, Rajarshi Das (In J. P. Crutch¯eld and P. K. Schuster (editors), Evolutionary Dynamics|Exploring the Interplay of Selection, Neutrality, Accident, and Function. New York: Oxford University Press, 2002.)
- The Evolution of Emergent Computation, James P. Crutchfield and Melanie Mitchell (SFI Technical Report 94-03-012)
- Ganguly, Sikdar, Deutsch and Chaudhuri "A Survey on Cellular Automata"
External links
- Berto, Francesco; Tagliabue, Jacopo. "Cellular Automata". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- Mirek's Cellebration – Home to free MCell and MJCell cellular automata explorer software and rule libraries. The software supports a large number of 1D and 2D rules. The site provides both an extensive rules lexicon and many image galleries loaded with examples of rules. MCell is a Windows application, while MJCell is a Java applet. Source code is available.
- Modern Cellular Automata – Easy to use interactive exhibits of live color 2D cellular automata, powered by Java applet. Included are exhibits of traditional, reversible, hexagonal, multiple step, fractal generating, and pattern generating rules. Thousands of rules are provided for viewing. Free software is available.
- Self-replication loops in Cellular Space – Java applet powered exhibits of self replication loops.
- A collection of over 10 different cellular automata applets (in Monash University's Virtual Lab)
- Golly supports von Neumann, Nobili, GOL, and a great many other systems of cellular automata. Developed by Tomas Rokicki and Andrew Trevorrow. This is the only simulator currently available that can demonstrate von Neumann type self-replication.
- Fourier Life - A collection of rules that demonstrate self-replicating patterns which spontaneously emerge from a field of random cells. Most of the rules were found using an algorithm that uses a Fourier transform to detect self-replication.
- Wolfram Atlas – An atlas of various types of one-dimensional cellular automata.
- Conway Life
- First replicating creature spawned in life simulator
- The Mathematics of the Models of Reference, featuring a general tutorial on CA, interactive applet, free code and resources on CA as model of fundamental physics
- Fourmilab Cellular Automata Laboratory
- Busy Boxes, a 3-D, reversible, SALT-architecture CA
- Cellular Automata Repository (CA researchers, historic links, free software, books and beyond)
- Cellular Automata in 256 Rules (A single sheet interactive visualization of 256 elementary rules )
- Petri -- a Go cellular automata framework


