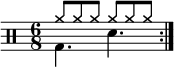Metre (music)

In music, metre (British spelling) or meter (American spelling) refers to regularly recurring patterns and accents such as
A variety of systems exist throughout the world for organising and playing metrical music, such as the Indian system of tala and similar systems in Arabic and African music.
Later music for
Metre is related to and distinguished from pulse, rhythm (grouping), and beats:
Meter is the measurement of the number of pulses between more or less regularly recurring accents. Therefore, in order for meter to exist, some of the pulses in a series must be accented—marked for consciousness—relative to others. When pulses are thus counted within a metric context, they are referred to as beats.[5]
Metric structure
The term metre is not very precisely defined.[1] Stewart MacPherson preferred to speak of "time" and "rhythmic shape",[6] while Imogen Holst preferred "measured rhythm".[7] However, Justin London has written a book about musical metre, which "involves our initial perception as well as subsequent anticipation of a series of beats that we abstract from the rhythm surface of the music as it unfolds in time".[8] This "perception" and "abstraction" of rhythmic bar is the foundation of human instinctive musical participation, as when we divide a series of identical clock-ticks into "tick–tock–tick–tock".[1] "Rhythms of recurrence" arise from the interaction of two levels of motion, the faster providing the pulse and the slower organizing the beats into repetitive groups.[9] In his book The Rhythms of Tonal Music, Joel Lester notes that, "[o]nce a metric hierarchy has been established, we, as listeners, will maintain that organization as long as minimal evidence is present".[10]

"Meter may be defined as a regular, recurring pattern of strong and weak beats. This recurring pattern of durations is identified at the beginning of a composition by a meter signature (time signature). ... Although meter is generally indicated by time signatures, it is important to realize that meter is not simply a matter of notation".
Frequently metres can be subdivided into a pattern of duples and triples.[12][1]
For example, a 3
4 metre consists of three units of a 2
8 pulse group, and a 6
8 metre consists of two units of a 3
8 pulse group. In turn, metric bars may comprise 'metric groups' - for example, a musical phrase or melody might consist of two bars x 3
4.[13]
The level of musical organisation implied by musical metre includes the most elementary levels of
- Metrical rhythm, by far the most common class in Western music, is where each time value is a multiple or fraction of a fixed unit (beat, see paragraph below), and normal divisive rhythm).
- Measured rhythm is where each time value is a multiple or fraction of a specified time unit but there are not regularly recurring accents (additive rhythm).
- Free rhythm is where the time values are not based on any fixed unit; since the time values lack a fixed unit, regularly recurring accents are no longer a possibility.
Some music, including
Metric structure includes metre,
Frequently encountered types of metre
This section needs additional citations for verification. (October 2020) |
Metres classified by the number of beats per measure
Duple and quadruple metre
In
For example, in the time signature 2
4, each bar contains two (2)
Corresponding quadruple metres are 4
4, which has four quarter-note beats per measure, and 12
8, which has four dotted-quarter-note beats per bar.
Triple metre
Triple metre is a metre in which each bar is divided into three beats, or a multiple thereof. For example, in the time signature 3
4, each bar contains three (3) quarter-note (4) beats, and with a time signature of 9
8, each bar contains three dotted-quarter beats.
More than four beats
Metres with more than four beats are called quintuple metres (5), sextuple metres (6), septuple metres (7), etc.
In classical music theory it is presumed that only divisions of two or three are perceptually valid, so a metre not divisible by 2 or 3, such as quintuple metre, say 5
4, is assumed to either be equivalent to a measure of 3
4 followed by a measure of 2
4, or the opposite: 2
4 then 3
4. Higher metres which are divisible by 2 or 3 are considered equivalent to groupings of duple or triple metre measures; thus, 6
4, for example, is rarely used because it is considered equivalent to two measures of 3
4. See: hypermetre and additive rhythm and divisive rhythm.
Higher metres are used more commonly in analysis, if not performance, of
8, the LCD of 4 and 3.
Metres classified by the subdivisions of a beat
Simple metre and compound metre are distinguished by the way the beats are subdivided.
Simple metre
Simple metre (or simple time) is a metre in which each beat of the bar divides naturally into two (as opposed to three) equal parts. The top number in the time signature will be 2, 3, 4, 5, etc.
For example, in the time signature 3
4, each bar contains three quarter-note beats, and each of those beats divides into two eighth notes, making it a simple metre. More specifically, it is a simple triple metre because there are three beats in each measure; simple duple (two beats) or simple quadruple (four) are also common metres.
Compound metre
Compound metre (or compound time), is a metre in which each beat of the bar divides naturally into three equal parts. That is, each beat contains a triple pulse.[18] The top number in the time signature will be 6, 9, 12, 15, 18, 24, etc.
Compound metres are written with a time signature that shows the number of divisions of beats in each bar as opposed to the number of beats. For example, compound duple (two beats, each divided into three) is written as a time signature with a numerator of six, for example, 6
8. Contrast this with the time signature 3
4, which also assigns six eighth notes to each measure, but by convention connotes a simple triple time: 3 quarter-note beats.
Examples of compound metre include 6
8 (compound duple metre), 9
8 (compound triple metre), and 12
8 (compound quadruple metre).
Although 3
4 and 6
8 are not to be confused, they use bars of the same length, so it is easy to "slip" between them just by shifting the location of the accents. This interpretational switch has been exploited, for example, by

Compound metre divided into three parts could theoretically be transcribed into musically equivalent simple metre using
8, conductors typically provide two beats per bar; however, all six beats may be performed when the tempo is very slow.
Compound time is associated with "lilting" and dancelike qualities. Folk dances often use compound time. Many Baroque dances are often in compound time: some gigues, the courante, and sometimes the passepied and the siciliana.
Metre in song

The concept of metre in music derives in large part from the
Traditional and popular songs may draw heavily upon a limited range of metres, leading to interchangeability of melodies. Early
In some regional music, for example
Metre in dance music


Metre is often essential to any style of dance music, such as the waltz or tango, that has instantly recognizable patterns of beats built upon a characteristic tempo and bar. The Imperial Society of Teachers of Dancing defines the tango, for example, as to be danced in 2
4 time at approximately 66 beats per minute. The basic slow step forwards or backwards, lasting for one beat, is called a "slow", so that a full "right–left" step is equal to one 2
4 bar.[24]
But step-figures such as turns, the corte and walk-ins also require "quick" steps of half the duration, each entire figure requiring 3–6 "slow" beats. Such figures may then be "amalgamated" to create a series of movements that may synchronise to an entire musical section or piece. This can be thought of as an equivalent of
Metre in classical music
In music of the common practice period (about 1600–1900), there are four different families of time signature in common use:
- duple: two or four beats to a bar, each divided by two, the top number being "2" or "4" (2
4, 2
8, 2
2 ... 4
4, 4
8, 4
2 ...). When there are four beats to a bar, it is alternatively referred to as "quadruple" time. - Simple triple: three beats to a bar, each divided by two, the top number being "3" (3
4, 3
8, 3
2 ...) - Compound duple: two beats to a bar, each divided by three, the top number being "6" (6
8, 6
16, 6
4 ...) Similarly compound quadruple, four beats to a bar, each divided by three, the top number being "12" (12
8, 12
16, 12
4 ...) - Compound triple: three beats to a bar, each divided by three, the top number being "9" (9
8, 9
16, 9
4)
If the beat is divided into two the metre is simple, if divided into three it is compound. If each bar is divided into two it is duple and if into three it is triple. Some people also label quadruple, while some consider it as two duples. Any other division is considered additively, as a bar of five beats may be broken into duple+triple (12123) or triple+duple (12312) depending on accent. However, in some music, especially at faster tempos, it may be treated as one unit of five.
Changing metre
In
![{ \new PianoStaff << \new Staff \relative c'' { \set Staff.midiInstrument = #"violin" \clef treble \tempo 8 = 126 \override DynamicLineSpanner.staff-padding = #4 \time 3/16 r16 <d c a fis d>-! r16\fermata | \time 2/16 r <d c a fis d>-! \time 3/16 r <d c a fis d>8-! | r16 <d c a fis d>8-! | \time 2/8 <d c a fis>16-! <e c bes g>->-![ <cis b aes f>-! <c a fis ees>-!] } \new Staff \relative c { \set Staff.midiInstrument = #"violin" \clef bass \time 3/16 d,16-! <bes'' ees,>^\f-! r\fermata | \time 2/16 <d,, d,>-! <bes'' ees,>-! | \time 3/16 d16-! <ees cis>8-! | r16 <ees cis>8-! | \time 2/8 d16^\sf-! <ees cis>-!->[ <d c>-! <d c>-!] } >> }](http://upload.wikimedia.org/score/k/d/kd0d2idcbjo5l4e03c969218icat3xx/kd0d2idc.png)
A metric modulation is a modulation from one metric unit or metre to another.
The use of
Hypermetre


Hypermetre is large-scale metre (as opposed to smaller-scale metre).
The term was coined, together with "hypermeasures", by Edward T. Cone (1968), who regarded it as applying to a relatively small scale, conceiving of a still larger kind of gestural "rhythm" imparting a sense of "an extended upbeat followed by its downbeat"[27] London (2012) contends that in terms of multiple and simultaneous levels of metrical "entrainment" (evenly spaced temporal events "that we internalize and come to expect", p. 9), there is no in-principle distinction between metre and hypermetre; instead, they are the same phenomenon occurring at different levels.[28]
4, 3
4, etc.) generate many different surface rhythms.[citation needed] For example, the first phrase of The Beatles' "A Hard Day's Night", excluding the syncopation on "night", may be generated from its metre of 4
4:[29]
The syncopation may then be added, moving "night" forward one eighth note, and the first phrase is generated.[citation needed]
Polymetre
With polymetre, the bar sizes differ, but the beat remains constant. Since the beat is the same, the various metres eventually agree. (Four bars of 7
4 = seven bars of 4
4). An example is the second moment, titled "Scherzo polimetrico", of Edmund Rubbra's Second String Quartet (1951), in which a constant triplet texture holds together overlapping bars of 9
8, 12
8, and 21
8, and barlines rarely coincide in all four instruments.[30]
With polyrhythm, the number of beats varies within a fixed bar length. For example, in a 4:3 polyrhythm, one part plays 4
4 while the other plays 3
4, but the 3
4 beats are stretched so that three beats of 3
4 are played in the same time as four beats of 4
4.[citation needed] More generally, sometimes rhythms are combined in a way that is neither tactus nor bar preserving—the beat differs and the bar size also differs. See Polytempi.[citation needed]
Research into the perception of polymetre shows that listeners often either extract a
In the music, the two metres will meet each other after a specific number of beats. For example, a 34 metre and 4
4 metre will meet after 12 beats.
In "Toads of the Short Forest" (from the album Weasels Ripped My Flesh), composer Frank Zappa explains: "At this very moment on stage we have drummer A playing in 7
8, drummer B playing in 3
4, the bass playing in 3
4, the organ playing in 5
8, the tambourine playing in 3
4,[clarification needed] and the alto sax blowing his nose".[33] "Touch And Go", a hit single by The Cars, has polymetric verses, with the drums and bass playing in 5
4, while the guitar, synthesizer, and vocals are in 4
4 (the choruses are entirely in 4
4).[34] Magma uses extensively 7
8 on 2
4 (e.g. Mëkanïk Dëstruktïẁ Kömmandöh) and some other combinations. King Crimson's albums of the eighties have several songs that use polymetre of various combinations.[citation needed]
Polymetres are a defining characteristic of the music of Meshuggah, whose compositions often feature unconventionally timed rhythm figures cycling over a 4
4 base.[35]
Examples
4 with 4 4 |
4 with 3 4 |
4 with 4 4 |
4 with 3 8 |
4 with 5 8 |
4 with 7 8 |
8 at tempo of 90 bpm |
8 at tempo of 90 bpm |
8 at tempo of 90 bpm |
4 at a tempo of 60 bpm |
4 at a tempo of 60 bpm |
4 at a tempo of 60 bpm |
See also
References
- ^ a b c d e f g Scholes 1977.
- ^ a b Latham 2002b.
- ^ Hoppin 1978, 221.
- ^ Merriam-Webster 2015.
- ^ Cooper & Meyer 1960, p. 3.
- ^ a b MacPherson 1930, 3.
- ^ Holst 1963, 17.
- ^ London 2004, 4.
- ^ Yeston 1976, 50–52.
- ^ Lester 1986, 77.
- ^ Benward and Saker 2003, 9.
- ^ a b MacPherson 1930, 5.
- ^ Cooper & Meyer 1960, p. [page needed].
- ^ Cooper 1973, 30.
- ^ Karpinski 2000, 19.
- ^ Forney and Machlis 2007, ?.
- ^ a b Wittlich 1975, ch. 3.
- ^ Latham 2002a.
- ^ Holst 1963, 18.
- ^ MacPherson 1930, 14.
- ^ London 2001, §I.8.
- ^ Read 1964, 147.
- ^ Scruton 1997.
- ^ Anon. 1983, p. [page needed].
- ^ Stein 2005, 329.
- ^ a b Neal 2000, 115.
- ^ Berry and Van Solkema 2013, §5(vi).
- ^ London 2012, 25.
- ^ Middleton 1990, 211.
- ^ Rubbra 1953, 41.
- ^ Boring 1942, 253.
- ^ London 2004, 49–50.
- ^ Mothers of Invention 1970.
- ^ Cars 1981, 15.
- ^ Pieslak 2007.
Sources
- Anon. (1983). Ballroom Dancing. Teach Yourself. ISBN 978-0-340-22517-2.
- Benward, Bruce, and Marilyn Nadine Saker (2003). Music: In Theory and Practice, Vol. 1, seventh edition. Boston: McGraw-Hill. ISBN 0-07-294262-2.
- Berry, David Carson, and Sherman Van Solkema (2013). "Theory". The Grove Dictionary of American Music, second edition, edited by Charles Hiroshi Garrett. New York: Oxford University Press. ISBN 978-0-19-531428-1.
- Boring, Edwin G. (1942). Sensation and Perception in the History of Experimental Psychology. New York: Appleton-Century.
- Cars, The (1981). Panorama (songbook). New York: Warner Bros. Publications.
- ISBN 978-0-39309767-2.
- Cooper, Grosvenor; )
- Cooper, Paul (1973). Perspectives in Music Theory: An Historical-Analytical Approach. New York: Dodd, Mead. ISBN 0-396-06752-2.
- Forney, Kristine, and Joseph Machlis (2007). The Enjoyment of Music: An Introduction to Perceptive Listening, tenth edition. New York: W. W. Norton. ISBN 978-0-393-10757-9(DVD)
- )
- Hoppin, Richard H. 1978. Medieval Music. New York: W. W. Norton. ISBN 0-393-09090-6.
- Karpinski, Gary S. (2000). Aural Skills Acquisition: The Development of Listening, Reading, and Performing Skills in College-Level Musicians. Oxford University Press. ISBN 0-19-511785-9.
- Krebs, Harald (2005). "Hypermeter and Hypermetric Irregularity in the Songs of Josephine Lang.". In Deborah Stein (ed.). Engaging Music: Essays in Music Analysis. New York: Oxford University Press. ISBN 0-19-517010-5.
- Latham, Alison (2002a). "Compound Time [Compound Metre]". In Alison Latham (ed.). The Oxford Companion to Music. Oxford and New York: Oxford University Press. ISBN 0-19-866212-2.
- Latham, Alison (2002b). "Metre". In Alison Latham (ed.). The Oxford Companion to Music. Oxford and New York: Oxford University Press. ISBN 0-19-866212-2.
- Lee, C. S. (1985). "The Rhythmic Interpretation of Simple Musical Sequences: Towards a Perceptual Model". In Peter Howell; Ian Cross; Robert West (eds.). Musical Structure and Cognition. London: Academic Press. ISBN 978-0-12357170-0.
- Lester, Joel (1986). The Rhythms of Tonal Music. Carbondale: Southern Illinois University Press. ISBN 0-8093-1282-4.
- London, Justin (2001). "Rhythm". In Stanley Sadie; John Tyrrell (eds.). The New Grove Dictionary of Music and Musicians (2nd ed.). London: Macmillan.
- London, Justin (2004). Hearing in Time: Psychological Aspects of Musical Meter (first ed.). Oxford: Oxford University Press. ISBN 0-19-516081-9.
- London, Justin (2012). Hearing in Time: Psychological Aspects of Musical Meter (second ed.). Oxford: Oxford University Press. ISBN 978-0-19-974437-4.
- MacPherson, Stewart (1930). Form in Music. London: Joseph Williams Ltd.
- Merriam-Webster (2015). "Measure". Dictionary. New York.
- ISBN 978-0-33515276-6.
- Mothers of Invention, The (1970), Weasels Ripped My Flesh (LP), Bizarre Records / Reprise Records, MS 2028 at Discogs (list of releases)
- Neal, Jocelyn (2000). "Songwriter's Signature, Artist's Imprint: The Metric Structure of a Country Song". In Wolfe, Charles K.; Akenson, James E. (eds.). Country Music Annual 2000. Lexington, KY: University Press of Kentucky. ISBN 0-8131-0989-2.
- Pieslak, Jonathan (2007). "Re-casting Metal: Rhythm and Meter in the Music of Meshuggah". .
- Read, Gardner (1964). Music Notation: A Manual of Modern Practice. Boston: Allyn and Bacon.
- Rubbra, Edmund (1953). "String Quartet No. 2 in E-flat, Op. 73: An Analytical Note by the Composer." The Music Review 14:36–44.
- Scholes, Percy (1977). John Owen Ward (ed.). The Oxford Companion to Music. 6th corrected reprint of the 10th ed. (1970), revised and reset. London and New York: Oxford University Press. ISBN 0-19-311306-6., chapters "Metre" and "Rhythm"
- ISBN 0-19-816638-9.
- Wittlich, Gary E., ed. (1975). Aspects of Twentieth-century Music. Englewood Cliffs, New Jersey: Prentice-Hall. ISBN 0-13-049346-5.
- ISBN 0-300-01884-3.
Further reading
- Anon. (1999). "Polymeter." Baker's Student Encyclopedia of Music, 3 vols., ed. Laura Kuhn. New York: Schirmer-Thomson Gale; London: Simon & Schuster.
- Anon. [2001]. "Polyrhythm". Grove Music Online. (Accessed 4 April 2009)
- ISBN 0-901938-16-5.
- Honing, Henkjan (2002). "Structure and Interpretation of Rhythm and Timing." Tijdschrift voor Muziektheorie 7(3):227–232. (pdf)
- Larson, Steve (2006). "Rhythmic Displacement in the Music of Bill Evans". In Structure and Meaning in Tonal Music: Festschrift in Honor of Carl Schachter, edited by L. Poundie Burstein and David Gagné, 103–122. Harmonologia Series, no. 12. Hillsdale, New York: Pendragon Press. ISBN 1-57647-112-8.
- Waters, Keith (1996). "Blurring the Barline: Metric Displacement in the Piano Solos of Herbie Hancock". Annual Review of Jazz Studies 8:19–37.

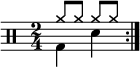



![\new Staff <<
\new voice \relative c' {
\clef percussion
\numericTimeSignature
\time 3/4
\set Score.tempoHideNote = ##t \tempo 4 = 100
\stemDown \repeat volta 2 { g4 d' d }
}
\new voice \relative c'' {
\override NoteHead.style = #'cross
\stemUp \repeat volta 2 { a8[ a] a[ a] a[ a] }
}
>>](http://upload.wikimedia.org/score/h/i/hi5b5unz1padlgy7b5jgghe9ncoqm7c/hi5b5unz.png)


![\new Staff <<
\new voice \relative c' {
\clef percussion
\numericTimeSignature
\time 3/4
\set Score.tempoHideNote = ##t \tempo 4 = 100
\stemDown \repeat volta 2 { g4 d' d }
}
\new voice \relative c'' {
\override NoteHead.style = #'cross
\stemUp \repeat volta 2 { a8[ a] a[ a] a[ a] }
}
>>](http://upload.wikimedia.org/score/q/0/q09k3q6mf4rqihq957lfeqnncvfjznl/q09k3q6m.png)