Quaquaversal tiling
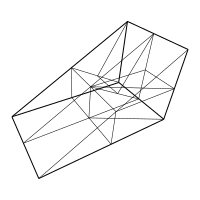
The quaquaversal tiling is a nonperiodic tiling of the Euclidean 3-space introduced by John Conway and Charles Radin. The basic solid tiles are half prisms arranged in a pattern that relies essentially on their previous construct, the pinwheel tiling.[1] The rotations relating these tiles belong to the group G(6,4) generated by two rotations of order 6 and 4 whose axes are perpendicular to each other. These rotations are dense in
SO(3).[2]
References
External links
- A picture of a quaquaversal tiling
- Charles Radin page at the University of Texas
  | ||||||
| ||||||
 | This geometry-related article is a stub. You can help Wikipedia by expanding it. |