Field (physics)

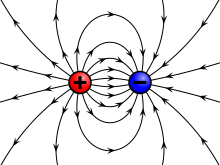
In

To

The development of the independent concept of a field truly began in the nineteenth century with the development of the theory of electromagnetism. In the early stages, André-Marie Ampère and Charles-Augustin de Coulomb could manage with Newton-style laws that expressed the forces between pairs of electric charges or electric currents. However, it became much more natural to take the field approach and express these laws in terms of electric and magnetic fields; in 1849 Michael Faraday became the first to coin the term "field".^[11]

The independent nature of the field became more apparent with

There are several examples of classical fields. Classical field theories remain useful wherever quantum properties do not arise, and can be active areas of research. Elasticity of materials, fluid dynamics and Maxwell's equations are cases in point.

Some of the simplest physical fields are vector force fields. Historically, the first time that fields were taken seriously was with

According to Newton's law of universal gravitation, F(r) is given by^[12]

${\displaystyle \mathbf {F} (\mathbf {r} )=-{\frac {GMm}{r^{2}}}{\hat {\mathbf {r} }},}$

where ${\displaystyle {\hat {\mathbf {r} }}}$ is a unit vector lying along the line joining M and m and pointing from M to m. Therefore, the gravitational field of M is^[12]

${\displaystyle \mathbf {g} (\mathbf {r} )={\frac {\mathbf {F} (\mathbf {r} )}{m}}=-{\frac {GM}{r^{2}}}{\hat {\mathbf {r} }}.}$

The experimental observation that inertial mass and gravitational mass are equal to an unprecedented level of accuracy leads to the identity that gravitational field strength is identical to the acceleration experienced by a particle. This is the starting point of the equivalence principle, which leads to general relativity.

Because the gravitational force F is

Michael Faraday first realized the importance of a field as a physical quantity, during his investigations into magnetism. He realized that electric and magnetic fields are not only fields of force which dictate the motion of particles, but also have an independent physical reality because they carry energy.

These ideas eventually led to the creation, by James Clerk Maxwell, of the first unified field theory in physics with the introduction of equations for the electromagnetic field. The modern version of these equations is called Maxwell's equations.

Electrostatics

A

A steady current I flowing along a path ℓ will create a field B, that exerts a force on nearby moving charged particles that is quantitatively different from the electric field force described above. The force exerted by I on a nearby charge q with velocity v is

${\displaystyle \mathbf {F} (\mathbf {r} )=q\mathbf {v} \times \mathbf {B} (\mathbf {r} ),}$

where B(r) is the magnetic field, which is determined from I by the Biot–Savart law:

${\displaystyle \mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\int {\frac {Id{\boldsymbol {\ell }}\times {\hat {\mathbf {r} }}}{r^{2}}}.}$

The magnetic field is not conservative in general, and hence cannot usually be written in terms of a scalar potential. However, it can be written in terms of a vector potential, A(r):

${\displaystyle \mathbf {B} (\mathbf {r} )={\boldsymbol {\nabla }}\times \mathbf {A} (\mathbf {r} )}$

Electrodynamics

In general, in the presence of both a charge density ρ(r, t) and current density J(r, t), there will be both an electric and a magnetic field, and both will vary in time. They are determined by Maxwell's equations, a set of differential equations which directly relate E and B to ρ and J.^[15]

Alternatively, one can describe the system in terms of its scalar and vector potentials V and A. A set of integral equations known as retarded potentials allow one to calculate V and A from ρ and J,^{[note 1]} and from there the electric and magnetic fields are determined via the relations^[16]

${\displaystyle \mathbf {E} =-{\boldsymbol {\nabla }}V-{\frac {\partial \mathbf {A} }{\partial t}}}$

${\displaystyle \mathbf {B} ={\boldsymbol {\nabla }}\times \mathbf {A} .}$

At the end of the 19th century, the electromagnetic field was understood as a collection of two vector fields in space. Nowadays, one recognizes this as a single antisymmetric 2nd-rank tensor field in spacetime.

Gravitation in general relativity

Einstein's theory of gravity, called general relativity, is another example of a field theory. Here the principal field is the metric tensor, a symmetric 2nd-rank tensor field in spacetime. This replaces Newton's law of universal gravitation.

Waves as fields

It is now believed that

In quantum chromodynamics, the color field lines are coupled at short distances by gluons, which are polarized by the field and line up with it. This effect increases within a short distance (around 1 fm from the vicinity of the quarks) making the color force increase within a short distance, confining the quarks within hadrons. As the field lines are pulled together tightly by gluons, they do not "bow" outwards as much as an electric field between electric charges.^[20]

These three quantum field theories can all be derived as special cases of the so-called

In

Field theory usually refers to a construction of the dynamics of a field, i.e., a specification of how a field changes with time or with respect to other independent physical variables on which the field depends. Usually this is done by writing a Lagrangian or a Hamiltonian of the field, and treating it as a classical or quantum mechanical system with an infinite number of degrees of freedom. The resulting field theories are referred to as classical or quantum field theories.

The dynamics of a classical field are usually specified by the Lagrangian density in terms of the field components; the dynamics can be obtained by using the action principle.

It is possible to construct simple fields without any prior knowledge of physics using only mathematics from

In a general setting, classical fields are described by sections of fiber bundles and their dynamics is formulated in the terms of jet manifolds (covariant classical field theory).^[21]

In

Symmetries of fields

A convenient way of classifying a field (classical or quantum) is by the

Spacetime symmetries

Fields are often classified by their behaviour under transformations of spacetime. The terms used in this classification are:

• scalar fields (such as temperature) whose values are given by a single variable at each point of space. This value does not change under transformations of space.
• force at each point in a magnetic field) which are specified by attaching a vector to each point of space. The components of this vector transform between themselves contravariantly
  under rotations in space. Similarly, a dual (or co-) vector field attaches a dual vector to each point of space, and the components of each dual vector transform covariantly.
• stress tensor
  of a crystal) specified by a tensor at each point of space. Under rotations in space, the components of the tensor transform in a more general way which depends on the number of covariant indices and contravariant indices.
• spinor fields (such as the Dirac spinor) arise in quantum field theory to describe particles with spin
  which transform like vectors except for one of their components; in other words, when one rotates a vector field 360 degrees around a specific axis, the vector field turns to itself; however, spinors would turn to their negatives in the same case.

Fields may have internal symmetries in addition to spacetime symmetries. In many situations, one needs fields which are a list of spacetime scalars: (φ₁, φ₂, ... φ_N). For example, in weather prediction these may be temperature, pressure, humidity, etc. In particle physics, the color symmetry of the interaction of quarks is an example of an internal symmetry, that of the strong interaction. Other examples are isospin, weak isospin, strangeness and any other flavour symmetry.

If there is a symmetry of the problem, not involving spacetime, under which these components transform into each other, then this set of symmetries is called an internal symmetry. One may also make a classification of the charges of the fields under internal symmetries.

Statistical field theory

Statistical field theory attempts to extend the field-theoretic paradigm toward many-body systems and statistical mechanics. As above, it can be approached by the usual infinite number of degrees of freedom argument.

Much like statistical mechanics has some overlap between quantum and classical mechanics, statistical field theory has links to both quantum and classical field theories, especially the former with which it shares many methods. One important example is

Continuous random fields

Classical fields as above, such as the

Notes

References

1. ISBN 0-297-81752-3
   .
2. ISBN 978-0-201-02115-8
   . A 'field' is any physical quantity which takes on different values at different points in space.
3. S2CID 27691986
   .
4. ^ SE, Windyty. "Windy as forecasted". Windy.com/. Retrieved 2021-06-25.
5. ^ Lecture 1 | Quantum Entanglements, Part 1 (Stanford), Leonard Susskind, Stanford, Video, 2006-09-25.
6. ^ Richard P. Feynman (1970). The Feynman Lectures on Physics Vol I. Addison Wesley Longman.
7. ^ Richard P. Feynman (1970). The Feynman Lectures on Physics Vol II. Addison Wesley Longman.
8. ISBN 9780393046427
   .
9. ^ Richard P. Feynman (1970). The Feynman Lectures on Physics Vol I. Addison Wesley Longman.
10. ^ Steven Weinberg (November 7, 2013). "Physics: What We Do and Don't Know". New York Review of Books.
11. ^
    JSTOR 20024506
    .
12. ^ ^{a b c} Kleppner, Daniel; Kolenkow, Robert. An Introduction to Mechanics. p. 85.
13. ^
    ISBN 0-07-051400-3
    .
14. ^
    ISBN 978-0-47-0746370
    .
15. ^ Griffiths, David. Introduction to Electrodynamics (3rd ed.). p. 326.
16. ^ Wangsness, Roald. Electromagnetic Fields (2nd ed.). p. 469.
17. ISBN 0-7167-0344-0
    .
18. ISBN 0-691-03323-4
    .
19. ISBN 0-201-50397-2.. Also see precision tests of QED
    .
20. ISBN 978-0-471-87373-0
    .
21. arXiv:0811.0331
    )

Further reading

• "Fields". Principles of Physical Science. Vol. 25 (15th ed.). 1994. p. 815. {{cite book}}: |work= ignored (help)
• ISBN 0-08-016019-0. Vol. 2 of the Course of Theoretical Physics
  .
• Jepsen, Kathryn (July 18, 2013). "Real talk: Everything is made of fields" (PDF). Symmetry Magazine. Archived from the original (PDF) on March 4, 2016. Retrieved June 9, 2015.

External links

Wikimedia Commons has media related to Field theory (physics).

• Particle and Polymer Field Theories