Список правильных многомерных многогранников и соединений

Примеры правильных многогранников

Правильные (2D) многоугольники
Выпуклые	Звёздчатые
{5}	{5/2}
Правильные 3D-многогранники
Выпуклые	Звёздчатые
{5,3}	{5/2,5}
Правильные 2D-замощения
Евклидовы	Гиперболические
{4,4}	{5,4}[англ.]
Правильные 4D-многогранники
Выпуклые	Звёздчатые
{5,3,3}	{5/2,5,3}[англ.]
Правильные 3D-замощения
Евклидовы	Гиперболические
{4,3,4}	{5,3,4}

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных соединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.

Символ Шлефли описывает каждое правильное замощение n-сферы, евклидова и гиперболического пространства. Символ Шлефли описания n-мерного многогранника равным образом описывает мозаику (n-1)-сферы. Вдобавок, симметрия правильного многогранника или замощения выражается как группа Коксетера, которые Коксетер обозначал идентично символам Шлефли, за исключением разграничения квадратными скобками, и эта нотация называется нотацией Коксетера^[англ.]. Другой связанный символ — диаграмма Коксетера — Дынкина, которая представляет группу симметрии (без помеченных кружком узлов) и правильные многогранники или замощения с обведённым кружком первым узлом. Например, куб имеет символ Шлефли {4,3}, с его октаэдральной симметрией^[англ.] [4,3] или , представляется диаграммой Коксетера .

Правильные многогранники сгруппированы по размерности, а затем по форме — выпуклые, невыпуклые и бесконечные. Невыпуклые виды используют те же вершины, что и выпуклые, но имеют пересекающиеся фасеты (грани максимальной размерности = размерности пространства – 1). Бесконечные виды

евклидово пространство на единицу меньшей размерности.

Бесконечные формы можно расширить до замощения гиперболического пространства. Гиперболическое пространство подобно обычному пространству, но параллельные прямые с расстоянием расходятся. Это позволяет вершинным фигурам иметь отрицательные угловые дефекты. Например, в вершине может сходиться семь правильных треугольников, лежащих на плоскости. Это нельзя осуществить на обычной (евклидовой) плоскости, но можно сделать при некотором масштабе на гиперболической плоскости.

Многогранники, удовлетворяющие более общему определению и не имеющие простых символов Шлефли, включают

.

Таблица показывает сводку правильных многогранников по размерностям.

	Конечные			Евклидовы	Гиперболические			Соединения
Разм.	Выпук- лые	Звёзд- чатые	Косые	Выпук- лые	Компак- тные	Звёзд- чатые	Параком- пактные	Выпук- лые	Звёзд- чатые
1	1	0	0	1	0	0	0	0	0
2	∞	∞	∞	1	1	0	0	∞	∞
3	5	4	?	3	∞	∞	∞	5	0
4	6	10	?	1	4	0	11	26	20
5	3	0	?	3	5	4	2	0	0
6	3	0	?	1	0	0	5	0	0
7	3	0	?	1	0	0	0	3	0
8	3	0	?	1	0	0	0	6	0
9+	3	0	?	1	0	0	0	*	0

* 1, если размерность имеет вид 2^k − 1; 2, если размерность является степенью двойки; 0 в противном случае.

Не существует правильных звёздчатых замощений в евклидовом пространстве любой размерности.

Диаграмма Коксетера — Дынкина представляет зеркальные "плоскости" как узлы, и помещает кружок вокруг узла, если точка не лежит на плоскости. Отрезок, { }, — это точка p и зеркальный образ точки p, а также отрезок между ними.

Одномерный многогранник (1-многогранник) — это замкнутый отрезок, ограниченный двумя конечными точками. 1-многогранник является правильным по определению и представляется символом Шлефли { }^[1][2] или диаграммой Коксетера с единственным помеченным кружком узлом, . Норман Джонсон дал им название дайтел и символ Шлефли { } ^[3].

Будучи тривиальным в качестве многогранника, дайтел возникает в качестве рёбер многоугольников и многогранников^[4]. Он используется в определении однородных призм (как в символе Шлефли { }×{p}) или в диаграмме Коксетера как прямое произведение отрезка и правильного многоугольника ^[5].

Двумерные многогранники называются многоугольниками. Правильные многоугольники имеют равные стороны и вписаны в окружность. Правильный p-угольник представляется символом Шлефли {p}.

Обычно только

можно также считать правильными. Они используют те же вершины, что и выпуклые формы, но соединение происходит другим путём, при котором окружность обходится более одного раза.

Звёздчатые многоугольники следует называть скорее невыпуклыми, чем вогнутыми, поскольку пересечение рёбер не образует новых вершин и все вершины находятся на окружности.

Выпуклые

Символ Шлефли {p} представляет правильный p-угольник.

Название	Треугольник (2-симплекс)	ортоплекс) (2-куб )	Пятиугольник	Шестиугольник	Семиугольник	Восьмиугольник
Шлефли	{3}	{4}	{5}	{6}	{7}	{8}
Симметрия	D3, [3]	D4, [4]	D5, [5]	D6, [6]	D7, [7]	D8, [8]
Коксетер
Рисунок
Название	Девятиугольник	Десятиугольник	Одиннадцатиугольник	Двенадцатиугольник	Тринадцатиугольник	Четырнадцатиугольник
Шлефли	{9}	{10}	{11}	{12}	{13}	{14}
Симметрия	D9, [9]	D10, [10]	D11, [11]	D12, [12]	D13, [13]	D14, [14]
Дынкин
Рисунок
Название	Пятнадцатиугольник	Шестнадцатиугольник	Семнадцатиугольник	Восемнадцатиугольник	Девятнадцатиугольник	Двадцатиугольник	...p-угольник
Шлефли	{15}	{16}	{17}	{18}	{19}	{20}	{p}
Симметрия	D15, [15]	D16, [16]	D17, [17]	D18, [18]	D19, [19]	D20, [20]	Dp, [p]
Дынкин
Рисунок

Правильный двуугольник {2} можно считать вырожденным правильным многоугольником. Он может существовать как невырожденный в некоторых неевклидовых пространствах, таких как поверхность сферы или тора.

Название	Одноугольник	Двуугольник
Символ Шлефли	{1}	{2}
Симметрия	D1, [ ]	D2, [2]
Коксетер diagram	или
Рисунок

Существует бесконечно много правильных звёздчатых многогранников в двумерном пространстве (т.е. многоугольников), символы Шлефли которых являются рациональными числами {n/m}. Они называются

, что и у выпуклого многоугольника.

В общем случае для любого натурального числа n и для всех m, таких, что m < n/2 и m, n взаимно просты, существуют n-точечные правильные звёзды с символами Шлефли {n/m} (строго говоря, {n/m}={n/(n−m)}) .

Название	Пентаграмма	Гептаграммы		Октаграмма	Эннеаграммы		Декаграмма[англ.]	... n-граммы
Шлефли	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{p/q}
Симметрия	D5, [5]	D7, [7]		D8, [8]	D9, [9],		D10, [10]	Dp, [p]
Коксетер
Рисунок

Правильные звёздчатые многоугольники с числом сторон до 20

{11/2}	{11/3}	{11/4}	{11/5}	{12/5}	{13/2}	{13/3}	{13/4}	{13/5}	{13/6}
{14/3}	{14/5}	{15/2}	{15/4}	{15/7}	{16/3}	{16/5}	{16/7}
{17/2}	{17/3}	{17/4}	{17/5}	{17/6}	{17/7}	{17/8}	{18/5}	{18/7}
{19/2}	{19/3}	{19/4}	{19/5}	{19/6}	{19/7}	{19/8}	{19/9}	{20/3}	{20/7}	{20/9}

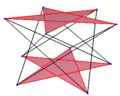
В 3-мерном пространстве правильный пространственный многоугольник ^[6] называется антипризматическим многоугольником и он имеет то же расположение вершин^[англ.], что и у антипризмы, и его рёбра являются подмножеством рёбер антипризмы, соединяющие зигзагом вершины верхнего и нижнего многоугольников.

Пример правильного пространственного зигзаг-многоугольника

Шестиугольник	Восьмиугольник	Десятиугольник
D3d, [2+,6]	D4d, [2+,8]	D5d, [2+,10]
{3}#{ }	{4}#{ }	{5}#{ }	{5/2}#{ }	{5/3}#{ }

В 4-мерном пространстве правильный пространственный многоугольник может иметь вершины на торе Клиффорда и связан с вращением Клиффорда^[англ.]. В отличие от антипризматичных пространственных многоугольников, пространственные многоугольники двойного вращения могут иметь нечётное число сторон.

Их можно видеть в многоугольниках Петри выпуклых правильных четырёхмерных многогранников^[англ.], видимые как правильные плоские многоугольники периметров проекций Коксетера:

Пятиугольник	Восьмиугольник	Двенадцатиугольник	Тридцатиугольник
Пятиячейник	Шестнадцатиячейник	Двадцатичетырёхъячейник	Шестисотячейник

В трёхмерном пространстве правильный многогранник с

{q}.

, эта вершинная фигура является всегда правильным (и планарным) многоугольником.

Существование правильного многогранника {p,q} ограничено неравенством, относящимся к угловому дефекту вершинной фигуры:

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}>{\frac {1}{2}}}$ : Многогранник (существует в евклидовом 3-мерном пространстве)

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}}$ : Евклидова плоская мозаика

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}}$ : Замощение гиперболической плоскости

Перенумеровав перестановки, мы найдём 5 выпуклых форм, 4 звёздчатые формы и 3 плоских замощения, все с многоугольниками {p} и {q} из списка: {3}, {4}, {5}, {5/2} и {6}.

Вдобавок к мозаикам евклидова пространства существует бесконечное количество правильных гиперболических мозаик.

Пять выпуклых правильных

(χ) 2.

Название	Шлефли {p,q}	Коксетер	Рисунок (прозрачный)	Рисунок (тело)	Рисунок (сфера)	Граней {p}	Рёбер	Вершин {q}	Симметрия	Двойственный
Тетраэдр (3-симплекс)	{3,3}					4 {3}	6	4 {3}	Td [3,3] (*332)	(самодвойственен)
Шестигранник Куб (3-куб)	{4,3}					6 {4}	12	8 {3}	Oh [4,3] (*432)	Октаэдр
ортоплекс )	{3,4}					8 {3}	12	6 {4}	Oh [4,3] (*432)	Куб
Додекаэдр	{5,3}					12 {5}	30	20 {3}	Ih [5,3] (*532)	Икосаэдр
Икосаэдр	{3,5}					20 {3}	30	12 {5}	Ih [5,3] (*532)	Додекаэдр

Сферические

В

.

Несколько первых примеров (n от 2 до 6) приведены ниже.

Осоэдры

Название	Шлефли {2,p}	Коксетер diagram	Рисунок (sphere)	Граней {2}π/p	Рёбер	Вершин {p}	Симметрия	Двойственный
Двуугольный осоэдр	{2,2}			2 {2}π/2	2	2 {2}π/2	D2h [2,2] (*222)	Самодвойственен
Треугольный осоэдр	{2,3}		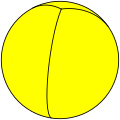	3 {2}π/3	3	2 {3}	D3h [2,3] (*322)	Треугольный диэдр
Квадратный осоэдр	{2,4}			4 {2}π/4	4	2 {4}	D4h [2,4] (*422)	Квадратный диэдр
Пятиугольный осоэдр	{2,5}			5 {2}π/5	5	2 {5}	D5h [2,5] (*522)	Пятиугольный диэдр
Шестиугольный осоэдр	{2,6}			6 {2}π/6	6	2 {6}	D6h [2,6] (*622)	Шестиугольный диэдр

Диэдры

Название	Шлефли {p,2}	Диаграмма Коксетера	Рисунок (сфера)	Граней {p}	Рёбер	Вершин {2}	Симметрия	Двойственный
Двуугольный диэдр	{2,2}			2 {2}π/2	2	2 {2}π/2	D2h [2,2] (*222)	Самодвойственен
Треугольный диэдр	{3,2}			2 {3}	3	3 {2}π/3	D3h [3,2] (*322)	Треугольный осоэдр
Квадратный диэдр	{4,2}		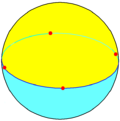	2 {4}	4	4 {2}π/4	D4h [4,2] (*422)	Квадратный осоэдр
Пятиугольный диэдр	{5,2}			2 {5}	5	5 {2}π/5	D5h [5,2] (*522)	Пятиугольный осоэдр
Шестиугольный диэдр	{6,2}			2 {6}	6	6 {2}π/6	D6h [6,2] (*622)	Шестиугольный осоэдр

Звёздчатые диэдры и осоэдры также существуют, такие как {5/2,2} и {2,5/2}.

Звёзды

Правильные

{3,5}:

Как сферические мозаики эти звёздчатые формы перекрывают сферу несколько раз, что называется их плотностью. Для этих форм плотность равна 3 или 7. Рисунки мозаик показывают грани отдельных сферических многоугольников жёлтым цветом.

Название	Рисунок (прозрачный)	Рисунок (непрозрачный)	Рисунок (сферический)	Диаграмма образования звёздчатой формы	Шлефли {p,q} и Коксетер	Граней {p}	Рёбер	Вершин {q} Фигура	χ	Плот- ность[англ.]	Симметрия	Двойственный
Малый звёздчатый додекаэдр					{5/2,5}	12 {5/2}	30	12 {5}	−6	3	Ih [5,3] (*532)	Большой додекаэдр
Большой додекаэдр					{5,5/2}	12 {5}	30	12 {5/2}	−6	3	Ih [5,3] (*532)	Малый звёздчатый додекаэдр
Большой звёздчатый додекаэдр					{5/2,3}	12 {5/2}	30	20 {3}	2	7	Ih [5,3] (*532)	Большой икосаэдр
Большой икосаэдр					{3,5/2}	20 {3}	30	12 {5/2}	2	7	Ih [5,3] (*532)	Большой звёздчатый додекаэдр

.

Для 4-мерных косых многогранников Коксетер предложил модифицированный

, представляющими зигзаги между двумя плоскостями.

Для правильных косых многогранников, представленных символом {l,m|n}, выполняется равенство:

2*sin(π/l)*sin(π/m)=cos(π/n)

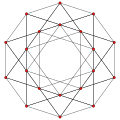
Четыре из них можно видеть в 4-мерном пространстве как множество граней четырёх правильных четырёхмерных многогранников, имеющих одно и то же расположение вершин^[англ.] и расположение рёбер^[англ.]:

{4, 6 | 3}	{6, 4 | 3}	{4, 8 | 3}	{8, 4 | 3}

Правильные

${\displaystyle \{p,q,r\}}$ имеют ячейки вида ${\displaystyle \{p,q\}}$, грани вида ${\displaystyle \{p\}}$, рёберные фигуры ${\displaystyle \{r\}}$ и вершинные фигуры ${\displaystyle \{q,r\}}$.

• Вершинная фигура
  (4-мерного многогранника) является (3-мерным) многогранником, образованным соседними к данной вершине вершинами многогранника. Для правильных четырёхмерных многогранников эта вершинная фигура является правильным (3-мерным) многогранником.
• Рёберной фигурой
  является многоугольник, образованный прилегающими к ребру гранями. Для правильных четырёхмерных многогранников рёберной фигурой всегда будет правильный многоугольник.

Существование правильных четырёхмерных многогранников ${\displaystyle \{p,q,r\}}$ ограничено существованием правильного многогранника ${\displaystyle \{p,q\},\{q,r\}}$. Для 4-мерных многогранников предлагается использовать название "полихор"[8]^[9]

Каждый вид может существовать в пространстве, зависящем от следующего выражения:

${\displaystyle \sin \left({\frac {\pi }{p}}\right)\sin \left({\frac {\pi }{r}}\right)-\cos \left({\frac {\pi }{q}}\right)}$

${\displaystyle >0}$ : Гиперсферические 3-мерные соты или 4-мерные многогранники

${\displaystyle =0}$ : евклидовы 3-мерные соты

${\displaystyle <0}$ : Гиперболические 3-мерные соты

Эти ограничения допустимы для 21 форм — 6 форм выпуклы, 10 не выпуклы, одна является евклидовыми 3-мерными сотами и 4 являются гиперболическими сотами.

Эйлерова характеристика ${\displaystyle \chi }$ четырёхмерного многогранника вычисляется по формуле ${\displaystyle \chi =V+F-E-C}$ и равна нулю для всех видов.

6 выпуклых правильных четырёхмерных многогранников показаны в таблице ниже. Все эти многогранники имеют эйлерову характеристику (χ) 0.

Название	Шлефли {p,q,r}	Коксетер	Ячейки[англ.] {p,q}	Граней {p}	Рёбер {r}	Вершин {q,r}	Двойственный {r,q,p}
Пятиячейник (4-симплекс)	{3,3,3}		5 {3,3}	10 {3}	10 {3}	5 {3,3}	(самодвойственен)
Тессеракт (4-куб)	{4,3,3}		8 {4,3}	24 {4}	32 {3}	16 {3,3}	Шестнадцатиячейник
ортоплекс )	{3,3,4}		16 {3,3}	32 {3}	24 {4}	8 {3,4}	Тессеракт
Двадцатичетырёхъячейник	{3,4,3}		24 {3,4}	96 {3}	96 {3}	24 {4,3}	(самодвойственен)
Стодвадцатиячейник	{5,3,3}		120 {5,3}	720 {5}	1200 {3}	600 {3,3}	Шестисотъячейник
Шестисотъячейник	{3,3,5}		600 {3,3}	1200 {3}	720 {5}	120 {3,5}	Стодвадцатиячейник

Пятиячейник	Тессеракт	Шестнадцати- ячейник	Двадцати- четырёхъячейник	Стодвадцати- ячейник	Шестисотъячейник
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
Каркас (Многоугольник Петри) в косой ортогональной проекции
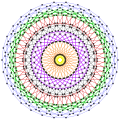
Ортогональная проекция
Тетраэдральная оболочка (центрировано по ячейке/вершине)	Кубическая оболочка (центрировано по ячейке)	Кубическая оболочка (центрировано по ячейке)	Кубооктаэдральная оболочка (центрировано по ячейке)	Усечённая ромботриаконта- эдральная оболочка[англ.] (центрировано по ячейке)	Пентакиикоси- додекаэдральная оболочка[англ.] (центрировано по вершине)
Диаграммы Шлегеля (перспективная проекция)
(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по вершине)
Каркас гиперсферический )

4-мерные

.

Правильные 4-мерные диэдры (2 фасеты = 3-мерные грани) включают: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2} и их двойственные 4-мерные осоэдры (2 вершины): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}, {2,2,p}. Многогранники вида {2,p,2} являются одновременно 4-мерными диэдрами и осоэдрами. Существуют также формы {p,2,q}, которые имеют диэдральные ячейки и осоэдральные вершинные фигуры.

Правильные 4-мерные осоэдры как соты на

3-сфере

Шлефли {2,p,q}	Коксетер	Ячейки[англ.] {2,p}π/q	Граней {2}π/p,π/q	Рёбер	Вершин	Вершинная фигура {p,q}	Симметрия	Двойственный
{2,3,3}		4 {2,3}π/3	6 {2}π/3,π/3	4	2	{3,3}	[2,3,3]	{3,3,2}
{2,4,3}		6 {2,4}π/3	12 {2}π/4,π/3	8	2	{4,3}	[2,4,3]	{3,4,2}
{2,3,4}		8 {2,3}π/4	12 {2}π/3,π/4	6	2	{3,4}	[2,4,3]	{4,3,2}
{2,5,3}		12 {2,5}π/3	30 {2}π/5,π/3	20	2	{5,3}	[2,5,3]	{3,5,2}
{2,3,5}		20 {2,3}π/5	30 {2}π/3,π/5	12	2	{3,5}	[2,5,3]	{5,3,2}

Существует десять

{3,3,5}.

Людвиг Шлефли нашёл четыре из них и отбросил остальные шесть, поскольку не позволял нарушение эйлеровой характеристики на ячейках или вершинных фигурах (F+V−E=2). Эдмунд Гесс (Edmund Hess, 1843–1903) завершил список в своей книге Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder ([3], 1883) (Введение в учение о замощении сферы с учётом теории равногранных и равноугольных многогранников) .

Существует 4 расположения рёбер^[англ.] и 7 расположений граней^[англ.] в этих 10 правильных звёздчатых 4-мерных многогранниках, показанные как ортогональные проекции:

Название	Каркас	Тело	Шлефли {p, q, r} Коксетер	Ячеек {p, q}	Граней {p}	Рёбер {r}	Вершин {q, r}	Плот- ность[англ.]	χ	Группа симметрии	Двойственный {r, q,p}
Икосаэдральный 120-ячейник[англ.] (огранённый Шестисотячейник)			{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2}	120 {5,5/2}	4	480	H4 [5,3,3]	Малый звёздчатый 120-ячейник
Малый звёздчатый 120-ячейник[англ.]			{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480	H4 [5,3,3]	Икосаэдральный 120-ячейник
Большой 120-ячейник[англ.]			{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0	H4 [5,3,3]	Самодвойственный
Великий 120-ячейник[англ.]			{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0	H4 [5,3,3]	Большой звёздчатый 120-ячейник
Большой звёздчатый 120-ячейник[англ.]			{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0	H4 [5,3,3]	Великий 120-ячейник
Великий звёздчатый 120-ячейник[англ.]			{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0	H4 [5,3,3]	Самодвойственный
Большой великий 120-ячейник[англ.]			{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480	H4 [5,3,3]	Большой икосаэдральный 120-ячейник
Большой икосаэдральный 120-ячейник[англ.] (большой огранёный 600-ячейник)			{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480	H4 [5,3,3]	Великий большой 120-ячейник
Великий 600-ячейник[англ.]			{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0	H4 [5,3,3]	Великий большой звёздчатый 120-ячейник
Большой великий 120-ячейник[англ.]			{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0	H4 [5,3,3]	Великий 600-ячейник

Существует 4 несостоявшихся правильных звёздчатых перестановок многогранников: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Их ячейки и вершинные фигуры существует, но они не покрывают гиперсферу конечным числом представлений.

В пятимерном пространстве^[англ.] правильные многогранники можно обозначить как ${\displaystyle \{p,q,r,s\}}$, где ${\displaystyle \{p,q,r\}}$ является типом 4-грани, ${\displaystyle \{p,q\}}$ является типом ячейки, ${\displaystyle \{p\}}$ является типом 2-грани, ${\displaystyle \{s\}}$ является фигурой грани, ${\displaystyle \{r,s\}}$ является рёберной фигурой, а ${\displaystyle \{q,r,s\}}$ является вершинной фигурой.

Вершинная фигура

(5-мерного многогранника) является 4-мерным многогранником, образованным вершинами, соседними с данной вершиной.

Рёберная фигура^[англ.] (5-мерного многогранника) является многогранником, образованным гранями вокруг каждого ребра.

Фигура грани^[англ.] (5-мерного многогранника) является многогранником, образованным ячейками вокруг каждой грани.

Правильный 5-мерный многогранник ${\displaystyle \{p,q,r,s\}}$ существует, только если ${\displaystyle \{p,q,r\}}$ и ${\displaystyle \{q,r,s\}}$ являются правильными четырёхмерными многогранниками.

В зависимости от значения

${\displaystyle {\frac {\cos ^{2}\left({\frac {\pi }{q}}\right)}{\sin ^{2}\left({\frac {\pi }{p}}\right)}}+{\frac {\cos ^{2}\left({\frac {\pi }{r}}\right)}{\sin ^{2}\left({\frac {\pi }{s}}\right)}}}$

получим тип пространства

${\displaystyle <1}$: Сферическое 4-мерное замощение или 5-мерный многогранник

${\displaystyle =1}$: евклидово 4-мерное замощение

${\displaystyle >1}$: Гиперболическое 4-мерное замощение

Из этих ограничений получаем 3 выпуклых многогранника, нуль невыпуклых многогранников, 3 4-мерных замощения и 5 гиперболических 4-мерных замощений. Не существует невыпуклых правильных многогранников в пятимерном пространстве и выше.

В размерностях 5 и выше существует только три вида выпуклых правильных многогранников ^[10].

Название	Символ Шлефли {p1,...,pn−1}	Коксетер	k-граней	Тип фасеты	Вершинная фигура	Двойственный
n-симплекс	{3n−1}	...	${\displaystyle {{n+1} \choose {k+1}}}$	{3n−2}	{3n−2}	Самодвойственен
n-куб	{4,3n−2}	...	${\displaystyle 2^{n-k}{n \choose k}}$	{4,3n−3}	{3n−2}	n-ортоплекс
n- ортоплекс	{3n−2,4}	...	${\displaystyle 2^{k+1}{n \choose {k+1}}}$	{3n−2}	{3n−3,4}	n-куб

Существуют также несобственные случаи, в которых некоторые числа в символе Шлефли равны 2. Например, {p,q,r,...2} является несобственным правильным сферическим многогранником в случае, если {p,q,r...} является правильным сферическим многогранником, и {2,...p,q,r} является несобственным правильным сферическим многогранником, когда {...p,q,r} является правильным сферическим многогранником. Такие многогранники можно использовать как фасеты, дающие формы вида {p,q,...2...y,z}.

Название	Символ Шлефли {p,q,r,s} Коксетер	Число фасет (четырёхмерных граней) {p,q,r}	Ячеек (трёхмерных граней) {p,q}	Граней (двумерных) {p}	Рёбер	Вершин	Фигура при грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}
Гексатерон	{3,3,3,3}	6 {3,3,3}	15 {3,3}	20 {3}	15	6	{3}	{3,3}	{3,3,3}
Пентеракт	{4,3,3,3}	10 {4,3,3}	40 {4,3}	80 {4}	80	32	{3}	{3,3}	{3,3,3}
5-ортоплекс	{3,3,3,4}	32 {3,3,3}	80 {3,3}	80 {3}	40	10	{4}	{3,4}	{3,3,4}

Гексатерон

Пентеракт

5-ортоплекс

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	χ
6-симплекс[англ.]	{3,3,3,3,3}	7	21	35	35	21	7	0
Хексеракт	{4,3,3,3,3}	64	192	240	160	60	12	0
6-ортоплекс[англ.]	{3,3,3,3,4}	12	60	160	240	192	64	0

6-мерный симплекс[англ.]

Хексеракт

6-мерный ортоплекс[англ.]

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	χ
7-симплекс[англ.]	{3,3,3,3,3,3}	8	28	56	70	56	28	8	2
Хептеракт	{4,3,3,3,3,3}	128	448	672	560	280	84	14	2
7-ортоплекс[англ.]	{3,3,3,3,3,4}	14	84	280	560	672	448	128	2

7-симплекс[англ.]

Хептеракт

7-ортоплекс[англ.]

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	χ
8-симплекс[англ.]	{3,3,3,3,3,3,3}	9	36	84	126	126	84	36	9	0
Октеракт	{4,3,3,3,3,3,3}	256	1024	1792	1792	1120	448	112	16	0
8-ортоплекс[англ.]	{3,3,3,3,3,3,4}	16	112	448	1120	1792	1792	1024	256	0

8-симплекс[англ.]

Октеракт

8-ортоплекс[англ.]

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	8D-граней	χ
9-симплекс[англ.]	{38}	10	45	120	210	252	210	120	45	10	2
Энтенеракт	{4,37}	512	2304	4608	5376	4032	2016	672	144	18	2
9-ортоплекс[англ.]	{37,4}	18	144	672	2016	4032	5376	4608	2304	512	2

9-симплекс[англ.]

Энтенеракт

9-ортоплекс[англ.]

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	8D-граней	9D-граней	χ
10-симплекс[англ.]	{39}	11	55	165	330	462	462	330	165	55	11	0
Декеракт	{4,38}	1024	5120	11520	15360	13440	8064	3360	960	180	20	0
10-ортоплекс[англ.]	{38,4}	20	180	960	3360	8064	13440	15360	11520	5120	1024	0

10-симплекс[англ.]

Декеракт

10-ортоплекс[англ.]

...

Не существует невыпуклых правильных многогранников в размерностях 5 и выше.

Проективный правильный (n+1)-многогранник существует, если исходное правильное n-сферическое замощение {p,q,...}

Правильные многоугольники с чётным числом сторон имеют полу-2n-угольные проективные многоугольники, {2p}/2.

Существует 4 правильных проективных многогранника^[англ.], соответствующих 4 из 5 платоновых тел.

Полукуб и полуоктаэдр обобщаются в полу-

в любой размерности.

3-dimensional regular hemi-polytopes

Название	Коксетер McMullen	Image	Faces	Edges	Vertices	χ
Полукуб[англ.]	{4,3}/2 {4,3}3		3	6	4	1
Полуоктаэдр[англ.]	{3,4}/2 {3,4}3		4	6	3	1
Полудодекаэдр	{5,3}/2 {5,3}5		6	15	10	1
Полуикосаэдр	{3,5}/2 {3,5}5		10	15	6	1

В 4-мерном пространстве 5 из 6 выпуклых правильных многогранников образуют проективные 4-мерные многогранники. 3 специальных случая — это полудвадцатичетырёхъячейник, полушестисотъячейник и полустодвадцатиячейник.

4-мерные правильные полумногогранники!Название

Символ
Коксетера

Символ
Макмаллена

Ячеек

Граней

Рёбер

Вершин

χ

полутессеракт	{4,3,3}/2	{4,3,3}4	4	12	16	8	0
полушестнадцатиячейник	{3,3,4}/2	{3,3,4}4	8	16	12	4	0
полудвадцатичетырёхъячейник	{3,4,3}/2	{3,4,3}6	12	48	48	12	0
полустодвадцатиячейник	{5,3,3}/2	{5,3,3}15	60	360	600	300	0
полу шестисотъячейник	{3,3,5}/2	{3,3,5}15	300	600	360	60	0

Существует только 2 выпуклых правильных проективных полумногогранника в пространствах размерности 5 и выше.

Название	Шлефли	4D-граней	Ячеек (3D)	Граней (2D)	Рёбер	Вершин	χ
полупентеракт	{4,3,3,3}/2	5	20	40	40	16	1
полупентакросс[англ.]	{3,3,3,4}/2	16	40	40	20	5	1

Бесконечногранник^[англ.] — это многогранник, имеющий бесконечное число фасет. n-бесконечногранник — это n-мерный бесконечногранник: 2-бесконечногранник = бесконечноугольник (апейрогон), 3-бесконечногранник = бесконечногранник в трёхмерном пространстве и т.д.

Существует два главных геометрических класса бесконечногранников:^[12]

• Правильные соты в n-мерном пространстве, полностью заполняющие n-мерное пространство.
• Правильные косые бесконечногранники^[англ.], содержащие n-мерные многообразия в более высоких пространствах.

Прямой апейрогон — это правильное замощение прямой с разделением её на бесконечно много равных отрезков. Он имеет бесконечно много вершин и рёбер. Его символ Шлефли равен {∞}, а диаграмма Коксетера — .

......

Апейрогоны на гиперболической плоскости, среди которых наиболее заметен правильный апейрогон {∞}, могут иметь кривизну, наподобие конечных многоугольников на евклидовой плоскости, и иметь вершины, лежащие на орициклах или гиперциклах.

Правильные апейрогоны со сходимостью на бесконечности имеют символ {∞} и существуют на орициклах, хотя в общем случае они могут существовать на гиперциклах.

{∞}	{πi/λ}
Бесконечноугольник на орицикле	Бесконечноугольник на гиперцикле

Выше показаны два гиперболических апейрогона на

, отстоящие на расстояние λ друг от друга.

Пространственные бесконечноугольники

Косые апейрогоны в двумерном пространстве (плоскости) образуют зигзаг. Если зигзаг симметричен и однороден, апейрогон правильный.

Косые апейрогоны можно построить в пространстве любой размерности. В трёхмерном пространстве косые апейрогоны^[англ.] образуют спираль и могут быть левыми или правыми.

Двумерное пространство	Трёхмерное пространство
Апейрогон в виде зигзага	Спиральный апейрогон

Существует три правильных замощения плоскости. Все три имеют эйлерову характеристику (χ) 0.

Название	Квадратная мозаика (кадриль)	Треугольная мозаика (дельтаплитка)	Шестиугольный паркет (гексаплитка)
Симметрия	p4m, [4,4], (*442)	p6m, [6,3], (*632)
Шлефли {p,q}	{4,4}	{3,6}	{6,3}
Диаграмма Коксетера
Рисунок

Существует две несобственные правильные мозаики — {∞,2}, бесконечноугольный диэдр, полученный из двух апейрогонов, каждый из которых заполняет полуплоскость, и двойственная ей {2,∞} мозаика, бесконечноугольный осоэдр, который можно представить как бесконечное число параллельных прямых.

{∞,2}[англ.],

{2,∞}[англ.],

Не существует правильных замощений плоскости

. Существует бесконечно много пар чисел, для которых выполняется условие плоской мозаики (1/p + 1/q = 1/2), например, {8/3,8}, {10/3,5}, {5/2,10}, {12/5,12}, и т.д., но ни одна из этих звёзд не подходит для замощения.

Замощения гиперболического двухмерного пространства — это гиперболические мозаики^[англ.]. Существует бесконечно много правильных мозаик в H². Как констатировано выше, любая положительная пара {p,q}, такая что 1/p + 1/q < 1/2 даёт гиперболическую мозаику. Фактически для общего треугольника Шварца (p, q, r) то же самое верно для 1/p + 1/q + 1/r < 1.

Существует много различных путей представления гиперболической плоскости, включая

.

Существует бесконечно много плоских правильных 3-бесконечногранников как правильных мозаик гиперболической плоскости, имеющих вид {p,q}, где p+q<pq/2.

• {3,7}, {3,8}, {3,9} ... {3,∞}
• {4,5}, {4,6}, {4,7} ... {4,∞}
• {5,4}, {5,5}, {5,6} ... {5,∞}
• {6,4}, {6,5}, {6,6} ... {6,∞}
• {7,3}, {7,4}, {7,5} ... {7,∞}
• {8,3}, {8,4}, {8,5} ... {8,∞}
• {9,3}, {9,4}, {9,5} ... {9,∞}
• ...
• {∞,3}, {∞,4}, {∞,5} ... {∞,∞}

Примеры:

Сферические (Платоновы)/Евклидовы/гиперболические (диск Пуанкаре: компактные/паракомпактные/некомпактные) замощения с их символами Шлефли
p \ q	3	4	5	6	7	8	...	∞	...	iπ/λ
3	(тетраэдр) {3,3}	(октаэдр) {3,4}	(икосаэдр) {3,5}	(дельта-плитка) {3,6}	{3,7}	{3,8}		{3,∞}		{3,iπ/λ}
4	(куб) {4,3}	(кадриль) {4,4}	{4,5}	{4,6}	{4,7}	{4,8}		{4,∞}		{4,iπ/λ}
5	додекаэдр ) {5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}		{5,∞}		{5,iπ/λ}
6	(гексаплитка) {6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}		{6,∞}		{6,iπ/λ}
7	{7,3}	{7,4}	{7,5}	{7,6}	{7,7}	{7,8}		{7,∞}		{7,iπ/λ}
8	{8,3}	{8,4}	{8,5}	{8,6}	{8,7}	{8,8}		{8,∞}		{8,iπ/λ}
...
∞	{∞,3}	{∞,4}	{∞,5}	{∞,6}	{∞,7}	{∞,8}	{∞,∞}	{∞,iπ/λ}
...
iπ/λ	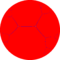{iπ/λ,3}	{iπ/λ,4}	{iπ/λ,5}	{iπ/λ,6}	{iπ/λ,7}	{iπ/λ,8}	{iπ/λ,∞}	{iπ/λ,iπ/λ}

Гиперболические звёздчатые мозаики

Существует два бесконечных вида гиперболических мозаик,

мозаик {m, 3}.

Схемы {m/2, m} и {m, m/2} продолжаются для нечётных m < 7 как многогранники: если m = 5, мы получим малый звёздчатый додекаэдр и большой додекаэдр, а при m = 3 мы получим тетраэдр. Другие два тела Кеплера — Пуансо (большой звёздчатый додекаэдр и большой икосаэдр) не имеют аналогов в правильных гиперболических мозаиках. Если m чётно, в зависимости от того, как мы выберем определение {m/2}, мы можем получить либо вырожденное покрытие другой мозаики или соединение мозаик.

Название	Шлефли	Диаграмма Коксетера	Рисунок	Тип грани {p}	Вершинная фигура {q}	Плот- ность[англ.]	Симметрия	Двойственная
Семиугольная мозаика порядка 7[англ.]	{7/2,7}			{7/2}	{7}	3	*732 [7,3]	Семиугольная гептаграммная мозаика
Семиугольная гептаграммная мозаика[англ.]	{7,7/2}			{7}	{7/2}	3	*732 [7,3]	Гептаграммная мозаика порядка7
Эннеаграммная мозаика порядка 9	{9/2,9}			{9/2}	{9}	3	*932 [9,3]	Эннеаграммная девятиугольная мозаика
Эннеаграммная девятиугольная мозаика	{9,9/2}			{9}	{9/2}	3	*932 [9,3]	Эннеаграммная девятиугольная мозаика порядка 9
Гендекаграммная мозаика порядка 11	{11/2,11}			{11/2}	{11}	3	*11.3.2 [11,3]	Гендекаграммная мозаика одиннадцатиугольная мозаика
Гендекаграммная мозаика одиннадцатиугольная мозаика	{11,11/2}			{11}	{11/2}	3	*11.3.2 [11,3]	Гендекаграммная мозаика порядка 11
p- граммная мозаика порядка p	{p/2,p}			{p/2}	{p}	3	*p32 [p,3]	p- граммная p- угольная мозаика
p-граммная мозаика p-угольная мозаика	{p,p/2}			{p}	{p/2}	3	*p32 [p,3]	p-граммная мозаика порядка p

Существует три

.

• 6 квадратов вокруг каждой вершины: {4,6|4}
• 4 шестиугольника вокруг каждой вершины: {6,4|4}
• 6 шестиугольников вокруг каждой вершины: {6,6|3}

кубических сот, {4,3,4} ^[16]. Оператор Петри^[англ.] π заменяет грани многоугольниками Петри

. δ является двойственным оператором, обменивающим местами вершины и грани. φ_k является k-м оператором огранки. η является оператором взятия половины, а σ — взятием косой половины.

Правильный косой многоугольник
{4,6|4}	{6,4|4}	{6,6|3}

Существует тридцать правильных бесконечноугольников в евклидовом трёхмерном пространстве [17]. Они включают как перечисленные выше, так и 8 других "чистых" бесконечноугольников. Все они связаны с кубическими сотами {4,3,4}. Остальные имеют пространственные многоугольные грани: {6,6}₄, {4,6}₄, {6,4}₆, {∞,3}^a, {∞,3}^b, {∞,4}^.*3, {∞,4}_6,4, {∞,6}_4,4 и {∞,6}_6,3.

Существует 31 правильный косой бесконечногранник^[англ.] в гиперболическом трёхмерном пространстве ^[18]:

• 14 компактных: {8,10|3}, {10,8|3}, {10,4|3}, {4,10|3}, {6,4|5}, {4,6|5}, {10,6|3}, {6,10|3}, {8,8|3}, {6,6|4}, {10,10|3},{6,6|5}, {8,6|3} и {6,8|3}.
• 17 паракомпактных: {12,10|3}, {10,12|3}, {12,4|3}, {4,12|3}, {6,4|6}, {4,6|6}, {8,4|4}, {4,8|4}, {12,6|3}, {6,12|3}, {12,12|3}, {6,6|6}, {8,6|4}, {6,8|4}, {12,8|3}, {8,12|3} и {8,8|4}.

Существует только одно невырожденное правильное замощение 3-мерного пространства (соты), {4, 3, 4} ^[19]:

Название	Шлефли {p,q,r}	Коксетер	Тип ячейки {p,q}	Тип грани {p}	Рёберная фигура {r}	Вершинная фигура {q,r}	χ	Двойственный
Кубические соты	{4,3,4}		{4,3}	{4}	{4}	{3,4}	0	Самодвойственны

Существует шесть несобственных правильных замощений, попарно основанных на трёх правильных евклидовых замощениях. Их ячейки и вершинные фигуры являются правильными осоэдрами {2,n}, диэдрами {n,2} и евклидовыми мозаиками. Эти несобственные правильные мозаики конструкционно связаны с призматическими однородными сотами операцией усечения. Они являются высокоразмерными аналогами бесконечноугольной мозаики порядка 2^[англ.] и бесконечноугольного осоэдра^[англ.].

Шлефли {p,q,r}	Диаграмма Коксетера	Тип ячейки {p,q}	Тип грани {p}	Рёберная фигура {r}	Вершинная фигура {q,r}
{2,4,4}[англ.]		{2,4}	{2}	{4}	{4,4}
{2,3,6}[англ.]		{2,3}	{2}	{6}	{3,6}
{2,6,3}		{2,6}	{2}	{3}	{6,3}
{4,4,2}		{4,4}	{4}	{2}	{4,2}
{3,6,2}		{3,6}	{3}	{2}	{6,2}
{6,3,2}		{6,3}	{6}	{2}	{3,2}

4 компактных правильных сот {5,3,4} {5,3,5}[англ.] {4,3,5}[англ.] {3,5,3}[англ.]

4 из 11 паракомпактных правильных сот {3,4,4} {3,6,3}[англ.] {4,4,3}[англ.] {4,4,4}[англ.]

Существует десять плоских правильных сот гиперболического 3-мерного пространства^[20] (перечислены выше как замощения):

• 4 компактных: {3,5,3}, {4,3,5}, {5,3,4} и {5,3,5}
• 6 паракомпактных: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} и {6,3,6}.

Замощения

. Существует 15 гиперболических сот в H³, 4 компактных и 11 паракомпактных.

Название	Символ Шлефли {p,q,r}	Коксетер	Тип ячейки {p,q}	Тип грани {p}	Рёберная фигура {r}	Вершинная фигура {q,r}	χ	Двойственный
Икосаэдральные соты[англ.]	{3,5,3}		{3,5}	{3}	{3}	{5,3}	0	Самодвойственны
Кубические соты порядка 5[англ.]	{4,3,5}		{4,3}	{4}	{5}	{3,5}	0	{5,3,4}
Додекаэдральные соты порядка 4	{5,3,4}		{5,3}	{5}	{4}	{3,4}	0	{4,3,5}
Додекаэдральные соты порядка 5[англ.]	{5,3,5}		{5,3}	{5}	{5}	{3,5}	0	Самодвойственны

Существует также 11 паракомпактных H³ сот (с бесконечными (евклидовыми) ячейками и/или вершинными фигурами): {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} и {6,3,6}.

Название	Символ Шлефли {p,q,r}	Коксетер	Тип ячейки {p,q}	Тпи грани {p}	Рёберная фигура {r}	Вершинная фигура {q,r}	χ	Двойственный
Тетраэдральные соты порядка 6[англ.]	{3,3,6}		{3,3}	{3}	{6}	{3,6}	0	{6,3,3}
Шестиугольные мозаичные соты[англ.]	{6,3,3}		{6,3}	{6}	{3}	{3,3}	0	{3,3,6}
Октаэдральные соты порядка 4	{3,4,4}		{3,4}	{3}	{4}	{4,4}	0	{4,4,3}
Квадратные мозаичные соты[англ.]	{4,4,3}		{4,4}	{4}	{3}	{4,3}	0	{3,3,4}
Треугольные мозаичные соты[англ.]	{3,6,3}		{3,6}	{3}	{3}	{6,3}	0	Самодвойственны
Кубические соты порядка 6[англ.]	{4,3,6}		{4,3}	{4}	{4}	{3,4}	0	{6,3,4}
Шестиугольные мозаичные соты порядка 4[англ.]	{6,3,4}		{6,3}	{6}	{4}	{3,4}	0	{4,3,6}
Квадратные мозаичные соты порядка 4[англ.]	{4,4,4}		{4,4}	{4}	{4}	{4,4}	0	{4,4,4}
Додекаэдральные соты порядка 6[англ.]	{5,3,6}		{5,3}	{5}	{5}	{3,5}	0	{6,3,5}
Шестиугольные мозаичные соты порядка 5[англ.]	{6,3,5}		{6,3}	{6}	{5}	{3,5}	0	{5,3,6}
Шестиугольные мозаичные соты порядка 6[англ.]	{6,3,6}		{6,3}	{6}	{6}	{3,6}	0	Самодвойственны

Некомпактные решения существуют как лоренцевы группы Коксетера и могут быть визуализированы с помощью открытой области в гиперболическом пространстве (фундаментальный тетраэдрон, имеющий некоторые части недостижимыми ввиду бесконечности), и некоторые нарисованы ниже, показывая их пересечение с плоскостью. Все соты, не показанные в таблицах и не имеющие двойки в их символе Шлефли, являются некомпактными.

Сферические/Евклидовы/гиперболические(компактные/паракомпактные/некомпактные) соты {p,3,r}

p \ r	3	4	5	6	7	8	... ∞
3	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	{3,3,∞}
4	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	{4,3,∞}
5	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	{5,3,∞}
6	{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{6,3,7}	{6,3,8}	{6,3,∞}
7	{7,3,3}	{7,3,4}	{7,3,5}	{7,3,6}	{7,3,7}	{7,3,8}	{7,3,∞}
8	{8,3,3}	{8,3,4}	{8,3,5}	{8,3,6}	{8,3,7}	{8,3,8}	{8,3,∞}
... ∞	{∞,3,3}	{∞,3,4}	{∞,3,5}	{∞,3,6}	{∞,3,7}	{∞,3,8}	{∞,3,∞}

q = 4	q = 5	q = 6
p \ r 3 4 5 3 {3,4,3} {3,4,4} {3,4,5} 4 {4,4,3} {4,4,4} {4,4,5} 5 {5,4,3} {5,4,4} {5,4,5}	p \ r 3 4 3 {3,5,3} {3,5,4} 4 {4,5,3} {4,5,4} 5 {5,5,3} {5,5,4}	p \ r 3 4 3 {3,6,3} {3,6,4} 4 {4,6,3} {4,6,4} 5 {5,6,3} {5,6,4}

Не существует гиперболических звёздчатых сот в H³ — все формы с правильным звёздчатым многогранником в качестве ячейки, вершинной фигуры, или того и другого оказываются сферическими.

Существует три вида бесконечных правильных (сот), которые могут заполнить евклидово четырёхмерное пространство:

Название	Символ Шлефли {p,q,r,s}	Тип фасеты {p,q,r}	Тип ячейки {p,q}	Тип грани {p}	Фигура грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}	Двойственный
Тессерактные соты[англ.]	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{4}	{3,4}	{3,3,4}	Самодвойственены
Шестнадцатиячейные соты	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,4,3,3}
Двадцати- четырёхъячейные соты	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{4,3,3}	{3,3,4,3}

Спроецированный фрагмент сот {4,3,3,4} (Тессерактовые соты)

Спроецированный фрагмент сот {3,3,4,3} (Шестнадцатиячейные соты)

Спроецированный фрагмент сот {3,4,3,3} (24-ячейные соты)

Существует также два несобственных случая, {4,3,4,2} и {2,4,3,4}. Существует три плоских правильных вида сот евклидова 4-мерного пространства:^[19]

• {4,3,3,4}, {3,3,4,3} и {3,4,3,3}.

Существует семь плоских правильных выпуклых сот гиперболического 4-мерного пространства:^[20]

• 5 компактных: {3,3,3,5}, {5,3,3,3}, {4,3,3,5}, {5,3,3,4}, {5,3,3,5}
• 2 паракомпактных: {3,4,3,4} и {4,3,4,3}.

Существует четыре плоских правильных звёздчатых видов сот в гиперболическом 4-мерном пространстве:^[20]

• {5/2,5,3,3}, {3,3,5,5/2}, {3,5,5/2,5} и {5,5/2,5,3}.

Существует семь выпуклых правильных сот и четыре звёздчатые формы сот в пространстве H^{4 [21]}. Пять выпуклых видов компактны, а два паракомпактны.

Пять компактных правильных сот в H⁴:

Название	Символ Шлефли {p,q,r,s}	Тип фасеты {p,q,r}	Тип ячейки {p,q}	Тип грани {p}	Фигура грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}	Двойственный
Пятиячейные соты порядка 5[англ.]	{3,3,3,5}	{3,3,3}	{3,3}	{3}	{5}	{3,5}	{3,3,5}	{5,3,3,3}
120-ячейные соты	{5,3,3,3}	{5,3,3}	{5,3}	{5}	{3}	{3,3}	{3,3,3}	{3,3,3,5}
Тессерактные соты порядка 5[англ.]	{4,3,3,5}	{4,3,3}	{4,3}	{4}	{5}	{3,5}	{3,3,5}	{5,3,3,4}
120-ячейные соты порядка 4[англ.]	{5,3,3,4}	{5,3,3}	{5,3}	{5}	{4}	{3,4}	{3,3,4}	{4,3,3,5}
120-ячейные соты порядка 5[англ.]	{5,3,3,5}	{5,3,3}	{5,3}	{5}	{5}	{3,5}	{3,3,5}	Самодвойственен

Два правильных паракомпактных правильных вида сот в H⁴: {3,4,3,4}, {4,3,4,3}.

Название	Символ Шлефли {p,q,r,s}	Тип фасеты {p,q,r}	Тип ячейки {p,q}	Тип грани {p}	Фигура грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}	Двойственный
24-ячейные соты порядка 4[англ.]	{3,4,3,4}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{4,3,4}	{4,3,4,3}
Кубические сотовые соты[англ.]	{4,3,4,3}	{4,3,4}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,4,3,4}

Некомпактные решения существуют как лоренцевы группы Коксетера и могут быть визуализированы с помощью открытой области в гиперболическом пространстве (фундаментальный пятиячейник, имеющий некоторые части недостижимыми ввиду бесконечности). Все соты, не показанные в таблицах и не имеющие двойки в их символе Шлефли, являются некомпактными.

Сферические/Евклидовы/гиперболические(компактные/паракомпактные/некомпактные) соты {p,q,r,s}

q=3, s=3 p \ r 3 4 5 3 {3,3,3,3} {3,3,4,3} {3,3,5,3} 4 {4,3,3,3} {4,3,4,3} {4,3,5,3} 5 {5,3,3,3} {5,3,4,3} {5,3,5,3}	q=3, s=4 p \ r 3 4 3 {3,3,3,4} {3,3,4,4} 4 {4,3,3,4} {4,3,4,4} 5 {5,3,3,4} {5,3,4,4}	q=3, s=5 p \ r 3 4 3 {3,3,3,5} {3,3,4,5} 4 {4,3,3,5} {4,3,4,5} 5 {5,3,3,5} {5,3,4,5}
q=4, s=3 p \ r 3 4 3 {3,4,3,3} {3,4,4,3} 4 {4,4,3,3} {4,3,4,3}	q=4, s=4 p \ r 3 4 3 {3,4,3,4} {3,4,4,4} 4 {4,4,3,4} {4,4,4,4}	q=4, s=5 p \ r 3 4 3 {3,4,3,5} {3,4,4,5} 4 {4,4,3,5} {4,4,4,5}

Существует четыре вида правильных звёздчатых сот в пространстве H⁴:

Название	Символ Шлефли {p,q,r,s}	Тип фасеты {p,q,r}	Тип ячейки type {p,q}	Тип грани {p}	Фигура грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}	Двойственный	Плот- ность
Соты из малого звёздчатого 120-ячейника[англ.]	{5/2,5,3,3}	{5/2,5,3}[англ.]	{5/2,5}	{5}	{5}	{3,3}	{5,3,3}	{3,3,5,5/2}	5
600-ячейник пентаграммного порядка[англ.]	{3,3,5,5/2}	{3,3,5}	{3,3}	{3}	{5/2}	{5,5/2}	{3,5,5/2}	{5/2,5,3,3}	5
Икосаэдральные 120-ячейные соты порядка 5[англ.]	{3,5,5/2,5}	{3,5,5/2}	{3,5}	{3}	{5}	{5/2,5}	{5,5/2,5}	{5,5/2,5,3}	10
Соты большого 120-ячейника[англ.]	{5,5/2,5,3}	{5,5/2,5}	{5,5/2}	{5}	{3}	{5,3}	{5/2,5,3}	{3,5,5/2,5}	10

Существуют только одни плоские правильные соты в евклидовом 5-мерном пространстве: ( перечислены выше как замощения) ^[19]

• {4,3,3,3,4}

Существует пять плоских правильных сот гиперболического 5-мерного пространства, все паракомпактные: (перечислены выше как замощения)^[20]

• {3,3,3,4,3}, {3,4,3,3,3}, {3,3,4,3,3}, {3,4,3,3,4} и {4,3,3,4,3}

Гиперкубические соты является единственным семейством правильных сот, которые могут замостить пространство любой размерности (пять и выше), образованные фасетами-гиперкубами, по четыре вокруг каждой (n-2)-мерной грани.

Название	Шлефли {p1, p2, ..., pn−1}	Тип фасеты	Вершинная фигура	Двойственный
Квадратный паркет	{4,4}	{4}	{4}	Самодвой- ственен
Кубические соты	{4,3,4}	{4,3}	{3,4}	Самодвой- ственны
Тессерактные соты[англ.]	{4,32,4}	{4,32}	{32,4}	Самодвой- ственны
5-кубические соты[англ.]	{4,33,4}	{4,33}	{33,4}	Самодвой- ственны
6-кубические соты[англ.]	{4,34,4}	{4,34}	{34,4}	Самодвой- ственны
7-кубические соты[англ.]	{4,35,4}	{4,35}	{35,4}	Самодвой- ственны
8-кубические соты[англ.]	{4,36,4}	{4,36}	{36,4}	Самодвой- ственны
n-мерные гиперкубические соты	{4,3n−2,4}	{4,3n−2}	{3n−2,4}	Самодвой- ственны

В E⁵ существуют также несобственные случаи {4,3,3,4,2}, {2,4,3,3,4}, {3,3,4,3,2}, {2,3,3,4,3}, {3,4,3,3,2} и {2,3,4,3,3}. В Eⁿ, {4,3ⁿ⁻³,4,2} и {2,4,3ⁿ⁻³,4} являются всегда несобственными евклидовыми замощениями.

Существует 5 правильных видов сот в H⁵, все паракомпактные. Они включают бесконечные (евклидовы) фасеты или вершинные фигуры: {3,4,3,3,3}, {3,3,4,3,3}, {3,3,3,4,3}, {3,4,3,3,4} и {4,3,3,4,3}.

Существует два некомпактных правильных замощения гиперболического пространстваразмерности 5 и выше и нет паракомпактных правильных замощений в гиперболическом пространстве размерности 6 и выше.

Название	Символ Шлефли {p,q,r,s,t}	Тип фасеты {p,q,r,s}	4-face type {p,q,r}	Cell type {p,q}	Face type {p}	Cell figure {t}	Face figure {s,t}	Edge figure {r,s,t}	Вершинная фигура {q,r,s,t}	Двойственный
5-ортоплексные соты[англ.]	{3,3,3,4,3}	{3,3,3,4}	{3,3,3}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,3}
Двадцати- четырёхъячейные сотовые соты	{3,4,3,3,3}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{3,3,3}	{4,3,3,3}	{3,3,3,4,3}
Шестнадцатиячейные сотовые соты	{3,3,4,3,3}	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{3,3}	{4,3,3}	{3,4,3,3}	Самодвой- ственны
24-ячейные соты порядка 4[англ.]	{3,4,3,3,4}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{3,3,4}	{4,3,3,4}[англ.]	{4,3,3,4,3}
Тессерактные сотовые соты[англ.]	{4,3,3,4,3}	{4,3,3,4}[англ.]	{4,3,3}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,4}

Поскольку не существует правильных звёздчатых n-многогранников для n ≥ 5, которые могли бы быть потенциальными ячейками или вершинными фигурами, не существует больше гиперболических звёздчатых сот в Hⁿ для n ≥ 5.

Не существует правильных компактных или паракомпактных замощений гиперболического пространства размерности 6 или выше. Все целые неперчисленные значения дают некомпактное замощение гиперболического n-мерного пространства.

Для любого натурального числа n существует n-вершинный звёздчатый правильный многоугольник с символом Шлефли {n/m} для любого m < n/2 (строго говоря, {n/m}={n/(n−m)}), где m и n взаимно просты. Если m и n не взаимно просты, полученный многоугольник будет иметь n/m сторон. Новая фигура получается вращением этих n/m-угольников на одну вершину (влево), пока число вращений не достигнет числа n/m минус единица, и комбинацией этих повёрнутых фигур. В экстремальном случае, когда n/m равно 2, получим фигуру из n/2 отрезков. Такая фигура называется вырожденным звёздчатым многоугольником.

В других случаях, когда n и m имеют общий делитель, получим звёздчатый многоугольник с меньшим n и с ним можно скомбинировать версии, полученные вращением. Эти фигуры называются звёздчатыми фигурами, несобственными звёздчатыми многоугольниками или соединениями многоугольников. Для них часто используется то же обозначение {n/m}, хотя некоторые авторы, такие как Грюнбаум (1994), предпочитают (с некоторыми уточнениями) форму k{n} как более правильную, где, обычно, k = m.

Следующее усложнение возникает, когда мы соединяем два или более звёздчатых многоугольника, как, например, две пентаграммы, отличающиеся поворотом на 36° и вписанные в десятиугольник. Правильнее в этом случае писать в виде k{n/m}, в нашем случае 2{5/2}, а не использовать обычно используемое {10/4}.

Расширенная нотация Коксетера для соединения многоугольников имеет вид c{m,n,...}[d{p,q,...}]e{s,t,...}, в которой отражается, что d различных {p,q,...} вместе покрывают вершины {m,n,...} c раз и грани {s,t,...} e раз. Если не существует правильного {m,n,...}, первая часть записи удаляется, оставляя [d{p,q,...}]e{s,t,...}. Противоположный случай — если не существует правильного {s,t,...}. Двойственным к of c{m,n,...}[d{p,q,...}]e{s,t,...} является e{t,s,...}[d{q,p,...}]c{n,m,...}. Если c или e равно 1, их можно опускать. Для соединения многоугольников эта нотация сводится к {nk}[k{n/m}]{nk}. Например, гексаграмму можно записать как {6}[2{3}]{6}.

Примеры для n=2..10, nk≤30

2{2}

3{2}

4{2}

5{2}

6{2}

7{2}

8{2}

9{2}

10{2}

11{2}

12{2}

13{2}

14{2}

15{2}

2{3}

3{3}

4{3}[англ.]

5{3}[англ.]

6{3}[англ.]

7{3}

8{3}

9{3}

10{3}

2{4}

3{4}[англ.]

4{4}[англ.]

5{4}[англ.]

6{4}

7{4}

2{5}[англ.]

3{5}[англ.]

4{5}[англ.]

5{5}

6{5}

2{5/2}

3{5/2}

4{5/2}

5{5/2}

6{5/2}

2{6}[англ.]

3{6}[англ.]

4{6}

5{6}

2{7}[англ.]

3{7}

4{7}

2{7/2}

3{7/2}

4{7/2}

2{7/3}

3{7/3}

4{7/3}

2{8}[англ.]

3{8}

2{8/3}

3{8/3}

2{9}[англ.]

3{9}

2{9/2}

3{9/2}

2{9/4}

3{9/4}

2{10}[англ.]

3{10}

2{10/3}

3{10/3}

2{11}

2{11/2}

2{11/3}

2{11/4}

2{11/5}

2{12}[англ.]

2{12/5}

2{13}

2{13/2}

2{13/3}

2{13/4}

2{13/5}

2{13/6}

2{14}

2{14/3}

2{14/5}

2{15}

2{15/2}

2{15/4}

2{15/7}

Правильные пространственные многоугольники также создают соединения, которые можно наблюдать в рёбрах призматического соединения антипризм^[англ.], например:

Правильные соединения пространственных многоугольников

Соединение пространственных квадратов		Соединение пространственных шестиугольников	Соединение пространственных десятиугольников
Два {2}#{ }	Три {2}#{ }	Два {3}#{ }	Два {5/3}#{ }

Правильные соединения многогранников можно определить как соединения, которые, подобно правильным многогранников, вершинно транзитивны, рёберно транзитивны^[англ.] и транзитивны по граням^[англ.]. По этому определению имеется 5 правильных соединений.

Симметрия	[4,3], Oh	[5,3]+, I	[5,3], Ih
Двойственность	Самодвойственный			Двойственные пары
Рисунок
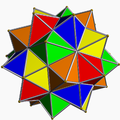
Сферические
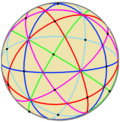
Многогранники	Звёздчатый октаэдр	5 {3,3}	10 {3,3}[англ.]	5 {4,3}[англ.]	5 {3,4}
Коксетер	{4,3}[2{3,3}]{3,4}	{5,3}[5{3,3}]{3,5}	2 {5,3}[10{3,3}]2{3,5}	2 {5,3}[5{4,3} ]	[5{3,4}]2{3,5}

Существует восемнадцать двупараметрических семейств правильных соединений мозаик евклидовой плоскости. На гиперболической плоскости известны пять однопараметрических семейств и семнадцать изолированных случаев, но полнота этого списка ещё не доказана.

Семейства соединений евклидовой и гиперболической плоскостей 2 {p,p} (4 ≤ p ≤ ∞, p целое) аналогичны сферическим звёздчатым октаэдрам, 2 {3,3}.

Несколько примеров евклидовых и гиперболических правильных соединений

Самодвойственные	Самодвойственные		Самодвойственные
2 {4,4}	2 {6,3}	2 {3,6}	2 {∞,∞}[англ.]
{{4,4}} или a{4,4} или {4,4}[2{4,4}]{4,4} + или	[2{6,3}]{3,6}	a{6,3} или {6,3}[2{3,6}] + или	{{∞,∞}} или a{∞,∞} или {4,∞}[2{∞,∞}]{∞,4} + или
	3 {6,3}	3 {3,6}	3 {∞,∞}[англ.]
	2{3,6}[3{6,3}]{6,3}	{3,6}[3{3,6}]2{6,3} + +	+ +

Ортогональные проекции

75 {4,3,3}	75 {3,3,4}

В 4-мерном пространстве существует тридцать два правильных соединения правильных многогранников, которые Коксетер перечислил в своей книге Regular Polytopes:^[22]

Самодвойственные правильные соединения

Соединение	Симметрия	Расположение вершин	Расположение ячеек
120 {3,3,3}	[5,3,3], порядок 14400	{5,3,3}	{3,3,5}
5 {3,4,3}	[5,3,3], порядок 14400	{3,3,5}	{5,3,3}

Правильные соединения как двойственные пары

Соединение 1	Соединение 2	Симметрия	Расположение вершин (1)	Расположение ячеек (1)	Расположение вершин (2)	Расположение ячеек (2)
3 {3,3,4}[23]	3 {4,3,3}	[3,4,3], порядок 1152	{3,4,3}	2{3,4,3}	2{3,4,3}	{3,4,3}
15 {3,3,4}	15 {4,3,3}	[5,3,3], порядок 14400	{3,3,5}	2{5,3,3}	2{3,3,5}	{5,3,3}
75 {3,3,4}	75 {4,3,3}	[5,3,3], порядок 14400	5{3,3,5}	10{5,3,3}	10{3,3,5}	5{5,3,3}
75 {3,3,4}	75 {4,3,3}	[5,3,3], порядок 14400	{5,3,3}	2{3,3,5}	2{5,3,3}	{3,3,5}
300 {3,3,4}	300 {4,3,3}	[5,3,3]+, порядок 7200	4{5,3,3}	8{3,3,5}	8{5,3,3}	4{3,3,5}
600 {3,3,4}	600 {4,3,3}	[5,3,3], порядок 14400	8{5,3,3}	16{3,3,5}	16{5,3,3}	8{3,3,5}
25 {3,4,3}	25 {3,4,3}	[5,3,3], порядок 14400	{5,3,3}	5{5,3,3}	5{3,3,5}	{3,3,5}

Существует два различных соединения 75 тессерактов: одно использует те же вершины, что и стодвадцатиячейник, а другое использует те же вершины, что и шестисотъячейник. Отсюда следует, что соответствующие двойственные соединения 75 шестнадцатиячейников также различны.

Самодвойственные звёздчатые соединения

Соединение	Симметрия	Расположение вершин	Расположение ячеек
5 {5,5/2,5}[англ.]	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}
10 {5,5/2,5}[англ.]	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}
5 {5/2,5,5/2}[англ.]	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}
10 {5/2,5,5/2}[англ.]	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}

Правильные звёздчатые соединения как двойственные пары

Соединение1	Соединение2	Симметрия	Расположение вершин (1)	Расположение ячеек (1)	Расположение вершин (2)	Расположение ячеек (2)
5 {3,5,5/2}[англ.]	5 {5/2,5,3}[англ.]	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {3,5,5/2}[англ.]	10 {5/2,5,3}[англ.]	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}
5 {5,5/2,3}[англ.]	5 {3,5/2,5}[англ.]	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {5,5/2,3}[англ.]	10 {3,5/2,5}[англ.]	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}
5 {5/2,3,5}[англ.]	5 {5,3,5/2}[англ.]	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {5/2,3,5}[англ.]	10 {5,3,5/2}[англ.]	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}

Существует также четырнадцать частично правильных соединений, которые либо вершинно-транзитивны, либо ячеечно-транзитивны, но не одновременно. Семь вершинно-транзитивных частично правильных соединений являются двойственными семи ячейно-транзитивным частично правильным соединениям.

Частично правильные соединения как двойственные пары

Соединение 1 вершинно транзитивны	Соединение 2 ячейно транзитивны[англ.]	Симметрия
2 шестнадцатиячейника [24]	2 тессеракта	[4,3,3], порядок 384
100 двадцатичетырёхъячейников	100 двадцатичетырёхъячейников	[5,3,3]+, порядок 7200
200 двадцатичетырёхъячейников	200 двадцатичетырёхъячейников	[5,3,3], порядок 14400
5 шестисотъячейников	5 стодвадцатиячейников	[5,3,3]+, порядок 7200
10 шестисотъячейников	10 стодвадцатиячейников	[5,3,3], порядок 14400

Частично правильные звёздчатые соединения как двойственные пары

Соединение1 вершинно транзитивны	Соединение2 ячейно транзитивны[англ.]	Симметрия
5 {3,3,5/2}[англ.]	5 {5/2,3,3}[англ.]	[5,3,3]+, порядок 7200
10 {3,3,5/2}[англ.]	10 {5/2,3,3}[англ.]	[5,3,3], порядок 14400

Единственными правильными евклидовыми соединениями сот является бесконечное семейство соединений

, имеющих общие вершины и грани с другими кубическими сотами. Это соединение может иметь любое число кубических сот. Запись Коксетера — {4,3,4}[d{4,3,4}]{4,3,4}.

Нет правильных соединений в пятимерном и шестимерном пространствах. Известны три семимерных соединения (16, 240 и 480 7-симплексов^[англ.]) и шесть восьмимерных (16, 240 и 480 октерактов или 8-ортоплексов^[англ.]). Существует также одно соединение n-мерных симплексов в n-мерном пространстве, при условии, что n на единицу меньше степени двойки, а также два соединения (соединение n-мерных кубов и двойственное ему соединение n-мерных ортоплексов) в n-мерном пространстве, если n является степенью двойки.

Запись Коксетера для этих соединений (где αⁿ = {3ⁿ⁻¹}, βⁿ = {3ⁿ⁻²,4}, γ_n = {4,3ⁿ⁻²}:

• 7-симплексы: cγ₇[16cα₇]cβ₇, where c = 1, 15 или 30
• 8-ортоплексы: cγ₈[16cβ₈]
• 8-кубы: [16cγ₈]cβ₈

Общий случай (когда n = 2^k and d = 2^{2k − k − 1}, k = 2, 3, 4, ...):

• Симплексы: γ_n−1[dα_n−1]β_n−1
• Ортоплексы: γ_n[dβ_n]
• Гиперкубы: [dγ_n]β_n

Известно бесконечное семейство правильных евклидовых соединений сот в размерностях пять и выше — соединение гиперкубических сот, разделяющих вершины и грани с другими гиперболическими сотами. Это соединение может иметь произвольное число гиперболических сот. Запись Коксетера для этих соединений — δ_n[dδ_n]δ_n where δ_n = {∞} при n = 2 и {4,3ⁿ⁻³,4} при n ≥ 3.

Понятие

, {5,3,5}, имеющие правильные проективные многогранники в качестве ячеек и вершинных фигур.

Элементами абстрактного многогранника являются его тело (максимальный элемент), грани, рёбра, вершины и нулевой многогранник (пустое множество). Эти абстрактные элементы могут быть отображены в обычное пространство или приняты как геометрические фигуры. Некоторые абстрактные многогранники имеют правильно построенную или правдоподобную реализацию, другие таковой не имеют. Флаг — это множество связанных элементов каждой размерности. Для четырёхмерного многогранника — это тело, грань, ребро этой грани, вершина ребра и нулевой многогранник. Говорят, что абстрактный многогранник является правильным, если его комбинаторные симметрии транзитивны на его флагах, то есть любой его флаг может быть переведён симметрией многогранника в любой другой. Абстрактные правильные многогранники являются активной областью исследований.

Пять таких правильных абстрактных многогранников, которые нельзя реализовать правдоподобно, были приведены Коксетером в его книге Regular Polytopes (1977), а затем в статье Уиллса (J. M. Wills) "The combinatorially regular polyhedra of index 2" (1987) ^[25]. Они топологически эквивалентны тороиду. Их построение путём расположения n граней около каждой вершины можно продолжать бесконечно, давая замощение гиперболической плоскости.

Многогранник	Средний Ромботриаконтаэдр	Додекододекаэдр	Средний триамбикикосаэдр[англ.]	Битригональный додекаэдр[англ.]	Выемчатый додекаэдр[англ.]
Вершинная фигура	{5}, {5/2}	(5.5/2)2	{5}, {5/2}	(5.5/3)3
Грани	30 ромбов	12 пятиугольников 12 пентаграмм	20 шестиугольников	12 пятиугольников 12 пентаграмм	20 гексаграмм
Мозаика	{4, 5}[англ.]	{5, 4}[англ.]	{6, 5}[англ.]	{5, 6}[англ.]	{6, 6}{6, 6}[англ.]
χ	−6	−6	−16	−16	−20

Они появляются как двойственные пары:

• Средний ромбический триаконтаэдр^[англ.] и додекододекаэдр двойственны друг другу.
• Средний триамбикикосаэдр^[англ.] и Битригональный додекаэдр^[англ.] двойственны друг другу.
• Выемчатый додекаэдр^[англ.] самодвойственен.

• Многоугольник
  • Правильный многоугольник
  • Звёздчатый многоугольник
• Многогранник
  • Правильный многогранник (5 правильных платоновых тел и 4 тела Кеплера — Пуансо)
    • Однородный многогранник
• Четырёхмерный многогранник
  • Правильный четырёхмерный многогранник (16 regular 4-polytopes, 4 convex and 10 star (Schläfli–Hess))
  • Однородный четырёхмерный многогранник^[англ.]
• Паркет (геометрия)
  • Замощение евклидовой плоскости правильными многоугольниками^[англ.]
  • Выпуклые однородные соты^[англ.]
• Правильные многомерные многогранники
  • Однородный четырёхмерный многогранник^[англ.]
• Правильная карта^[англ.]

• Платоновы тела
• тела Кеплера — Пуансо
• Regular 4d Polytope Foldouts
• Multidimensional Glossary (См. Hexacosichoron и Hecatonicosachoron)
• Polytope Viewer
• Polytopes and optimal packing of p points in n dimensional spheres
• Атлас малых правильных многогранников
• Regular polyhedra through time I. Hubard, Polytopes, Maps and their Symmetries

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии. Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником.