Quantum mechanics: Difference between revisions
79,664 edits Reverted 1 pending edit by 41.115.20.34 to revision 948973826 by AquaDTRS |
m →History: Fixed reference position |
||
| Line 62: | Line 62: | ||
It was found that [[subatomic particles]] and electromagnetic waves are neither simply particle nor wave but have certain properties of each. This originated the concept of [[wave–particle duality]].<ref name= feynmanIII /> |
It was found that [[subatomic particles]] and electromagnetic waves are neither simply particle nor wave but have certain properties of each. This originated the concept of [[wave–particle duality]].<ref name= feynmanIII /> |
||
By 1930, quantum mechanics had been further unified and formalized by [[David Hilbert]], [[Paul Dirac]] and [[John von Neumann]]<ref>{{cite journal|last=van Hove|first=Leon|title=Von Neumann's contributions to quantum mechanics|journal=Bulletin of the American Mathematical Society|year=1958|volume=64|issue=3|pages =Part 2:95–99 |url=http://www.ams.org/journals/bull/1958-64-03/S0002-9904-1958-10206-2/S0002-9904-1958-10206-2.pdf |doi=10.1090/s0002-9904-1958-10206-2}}</ref> with greater emphasis on [[measurement in quantum mechanics|measurement]], the statistical nature of our knowledge of reality, and [[Interpretations of quantum mechanics|philosophical speculation about the 'observer']]<ref name= "NKS note a">''[[A New Kind of Science]]'' [https://www.wolframscience.com/nks/notes-9-16--quantum-effects/ Note (a) for Quantum phenomena]</ref> |
By 1930, quantum mechanics had been further unified and formalized by [[David Hilbert]], [[Paul Dirac]] and [[John von Neumann]]<ref>{{cite journal|last=van Hove|first=Leon|title=Von Neumann's contributions to quantum mechanics|journal=Bulletin of the American Mathematical Society|year=1958|volume=64|issue=3|pages =Part 2:95–99 |url=http://www.ams.org/journals/bull/1958-64-03/S0002-9904-1958-10206-2/S0002-9904-1958-10206-2.pdf |doi=10.1090/s0002-9904-1958-10206-2}}</ref> with greater emphasis on [[measurement in quantum mechanics|measurement]], the statistical nature of our knowledge of reality, and [[Interpretations of quantum mechanics|philosophical speculation about the 'observer']].<ref name= "NKS note a">''[[A New Kind of Science]]'' [https://www.wolframscience.com/nks/notes-9-16--quantum-effects/ Note (a) for Quantum phenomena]</ref> It has since permeated many disciplines, including quantum chemistry, [[quantum electronics]], [[quantum optics]], and [[quantum information science]]. It also provides a useful framework for many features of the modern [[periodic table|periodic table of elements]], and describes the behaviors of [[atoms]] during [[chemical bond]]ing and the flow of [[electron]]s in computer [[semiconductor]]s, and therefore plays a crucial role in many modern technologies.<ref name="feynmanIII" /> Its speculative modern developments include [[string theory]] and [[quantum gravity]] theory. |
||
While quantum mechanics was constructed to describe the world of the very small, it is also needed to explain some [[macroscopic]] phenomena such as [[superconductivity|superconductors]]<ref name= feynman2015 >{{cite web |url=http://www.feynmanlectures.caltech.edu/III_21.html#Ch21-S5 |title= The Feynman Lectures on Physics '''III''' 21-4 |quote="...it was long believed that the wave function of the Schrödinger equation would never have a macroscopic representation analogous to the macroscopic representation of the amplitude for photons. On the other hand, it is now realized that the phenomena of superconductivity presents us with just this situation. |last=Feynman |first= Richard|authorlink= Richard Feynman |publisher= [[California Institute of Technology]] |accessdate=2015-11-24}}</ref> and [[superfluid]]s.<ref>[http://physics.berkeley.edu/sites/default/files/_/lt24_berk_expts_on_macro_sup_effects.pdf Richard Packard (2006) "Berkeley Experiments on Superfluid Macroscopic Quantum Effects" ]{{webarchive |url=https://web.archive.org/web/20151125112132/http://research.physics.berkeley.edu/packard/publications/Articles/LT24_Berk_expts_on_macro_sup_effects.pdf |date=November 25, 2015 }} accessdate=2015-11-24</ref> |
While quantum mechanics was constructed to describe the world of the very small, it is also needed to explain some [[macroscopic]] phenomena such as [[superconductivity|superconductors]]<ref name= feynman2015 >{{cite web |url=http://www.feynmanlectures.caltech.edu/III_21.html#Ch21-S5 |title= The Feynman Lectures on Physics '''III''' 21-4 |quote="...it was long believed that the wave function of the Schrödinger equation would never have a macroscopic representation analogous to the macroscopic representation of the amplitude for photons. On the other hand, it is now realized that the phenomena of superconductivity presents us with just this situation. |last=Feynman |first= Richard|authorlink= Richard Feynman |publisher= [[California Institute of Technology]] |accessdate=2015-11-24}}</ref> and [[superfluid]]s.<ref>[http://physics.berkeley.edu/sites/default/files/_/lt24_berk_expts_on_macro_sup_effects.pdf Richard Packard (2006) "Berkeley Experiments on Superfluid Macroscopic Quantum Effects" ]{{webarchive |url=https://web.archive.org/web/20151125112132/http://research.physics.berkeley.edu/packard/publications/Articles/LT24_Berk_expts_on_macro_sup_effects.pdf |date=November 25, 2015 }} accessdate=2015-11-24</ref> |
||
Revision as of 14:48, 10 April 2020
| Part of a series of articles about |
| Quantum mechanics |
|---|
Quantum mechanics (QM; also known as quantum physics, quantum theory, the wave mechanical model, or matrix mechanics), including quantum field theory, is a fundamental theory in physics describing the properties of nature on an atomic scale.[2]
Quantum mechanics
History
| Modern physics |
|---|
| |
Scientific inquiry into the wave nature of light began in the 17th and 18th centuries, when scientists such as
In 1838, Michael Faraday discovered cathode rays. These studies were followed by the 1859 statement of the black-body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system can be discrete, and the 1900 quantum hypothesis of Max Planck.[7] Planck's hypothesis that energy is radiated and absorbed in discrete "quanta" (or energy packets) precisely matched the observed patterns of black-body radiation.
In 1896, Wilhelm Wien empirically determined a distribution law of black-body radiation,[8] called Wien's law. Ludwig Boltzmann independently arrived at this result by considerations of Maxwell's equations. However, it was valid only at high frequencies and underestimated the radiance at low frequencies.
The foundations of quantum mechanics were established during the first half of the 20th century by Max Planck, Niels Bohr, Werner Heisenberg, Louis de Broglie, Arthur Compton, Albert Einstein, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Enrico Fermi, Wolfgang Pauli, Max von Laue, Freeman Dyson, David Hilbert, Wilhelm Wien, Satyendra Nath Bose, Arnold Sommerfeld, and others. The Copenhagen interpretation of Niels Bohr became widely accepted.
Among the first to study quantum phenomena were
According to Planck, each energy element (E) is proportional to its frequency (ν):
- ,

where h is Planck's constant.
Planck cautiously insisted that this was only an aspect of the processes of absorption and emission of radiation and was not the physical reality of the radiation.
Einstein further developed this idea to show that an

In the mid-1920s, quantum mechanics was developed to become the standard formulation for atomic physics. In the summer of 1925, Bohr and Heisenberg published results that closed the old quantum theory. Due to their particle-like behavior in certain processes and measurements, light quanta came to be called
It was found that
By 1930, quantum mechanics had been further unified and formalized by
While quantum mechanics was constructed to describe the world of the very small, it is also needed to explain some
The word quantum derives from the
Quantum mechanics is essential for understanding the behavior of systems at atomic length scales and smaller. If the physical nature of an atom were solely described by classical mechanics, electrons would not orbit the nucleus, since orbiting electrons emit radiation (due to circular motion) and so would quickly lose energy and collide with the nucleus. This framework was unable to explain the stability of atoms. Instead, electrons remain in an uncertain, non-deterministic, smeared, probabilistic wave–particle orbital about the nucleus, defying the traditional assumptions of classical mechanics and electromagnetism.[26]
Quantum mechanics was initially developed to provide a better explanation and description of the atom, especially the differences in the spectra of light emitted by different isotopes of the same chemical element, as well as subatomic particles. In short, the quantum-mechanical atomic model has succeeded spectacularly in the realm where classical mechanics and electromagnetism falter.
Broadly speaking, quantum mechanics incorporates four classes of phenomena for which classical physics cannot account[20]:
- certain physical properties
- quantum entanglement
- principle of uncertainty
- wave–particle duality
Mathematical formulations
In the mathematically rigorous formulation of quantum mechanics developed by
In the formalism of quantum mechanics, the state of a system at a given time is described by a complex wave function, also referred to as state vector in a complex vector space.[32] This abstract mathematical object allows for the calculation of probabilities of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one can never make simultaneous predictions of conjugate variables, such as position and momentum, to arbitrary precision. For instance, electrons may be considered (to a certain probability) to be located somewhere within a given region of space, but with their exact positions unknown. Contours of constant probability density, often referred to as "clouds", may be drawn around the nucleus of an atom to conceptualize where the electron might be located with the most probability. Heisenberg's uncertainty principle quantifies the inability to precisely locate the particle given its conjugate momentum.[33]
According to one interpretation, as the result of a measurement, the wave function containing the probability information for a system
The
Generally, quantum mechanics does not assign definite values. Instead, it makes a prediction using a
In the everyday world, it is natural and intuitive to think of everything (every observable) as being in an eigenstate. Everything appears to have a definite position, a definite momentum, a definite energy, and a definite time of occurrence. However, quantum mechanics does not pinpoint the exact values of a particle's position and momentum (since they are conjugate pairs) or its energy and time (since they too are conjugate pairs). Rather, it provides only a range of probabilities in which that particle might be given its momentum and momentum probability. Therefore, it is helpful to use different words to describe states having uncertain values and states having definite values (eigenstates).
Usually, a system will not be in an
For example, the free particle in the previous example will usually have a wave function that is a wave packet centered around some mean position x0 (neither an eigenstate of position nor of momentum). When one measures the position of the particle, it is impossible to predict with certainty the result.[34] It is probable, but not certain, that it will be near x0, where the amplitude of the wave function is large. After the measurement is performed, having obtained some result x, the wave function collapses into a position eigenstate centered at x.[39]
The time evolution of a quantum state is described by the
During a
Wave functions change as time progresses. The
Some wave functions produce probability distributions that are constant, or independent of time – such as when in a
The Schrödinger equation acts on the entire probability amplitude, not merely its absolute value. Whereas the absolute value of the probability amplitude encodes information about probabilities, its
Analytic solutions of the Schrödinger equation are known for very few relatively simple model Hamiltonians including the quantum harmonic oscillator, the particle in a box, the dihydrogen cation, and the hydrogen atom. Even the helium atom – which contains just two electrons – has defied all attempts at a fully analytic treatment.
However, there are techniques for finding approximate solutions. One method, called perturbation theory, uses the analytic result for a simple quantum mechanical model to create a result for a related but more complicated model by (for example) the addition of a weak potential energy. Another method is called "semi-classical equation of motion", which applies to systems for which quantum mechanics produces only small deviations from classical behavior. These deviations can then be computed based on the classical motion. This approach is particularly important in the field of quantum chaos.
Mathematically equivalent formulations
There are many mathematically equivalent formulations of quantum mechanics. One of the oldest and most common is the "transformation theory" proposed by Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics – matrix mechanics (invented by Werner Heisenberg) and wave mechanics (invented by Erwin Schrödinger).[45]
Especially since Heisenberg was awarded the
Relation to other scientific theories
The rules of quantum mechanics are fundamental. They assert that the state space of a system is a
In the
When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the classical harmonic oscillator.
Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein–Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field (rather than a fixed set of particles). The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction. The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one that has been used since the inception of quantum mechanics, is to treat charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
It has proven difficult to construct quantum models of
Classical mechanics has also been extended into the
Relation to classical physics
Predictions of quantum mechanics have been verified experimentally to an extremely high degree of
- Many macroscopic properties of a classical system are a direct consequence of the quantum behavior of its parts. For example, the stability of bulk matter (consisting of atoms and molecules which would quickly collapse under electric forces alone), the rigidity of solids, and the mechanical, thermal, chemical, optical and magnetic properties of matter are all results of the interaction of electric charges under the rules of quantum mechanics.[57]
- While the seemingly "exotic" behavior of matter posited by quantum mechanics and relativity theory become more apparent for extremely small particles or for velocities approaching the speed of light, the laws of classical, often considered "Newtonian", physics remain accurate in predicting the behavior of the vast majority of "large" objects (on the order of the size of large molecules or bigger) at velocities much smaller than the velocity of light.[58]
Copenhagen interpretation of quantum versus classical kinematics
A big difference between classical and quantum mechanics is that they use very different kinematic descriptions.[59]
In Niels Bohr's mature view, quantum mechanical phenomena are required to be experiments, with complete descriptions of all the devices for the system, preparative, intermediary, and finally measuring. The descriptions are in macroscopic terms, expressed in ordinary language, supplemented with the concepts of classical mechanics.[60][61][62][63] The initial condition and the final condition of the system are respectively described by values in a configuration space, for example a position space, or some equivalent space such as a momentum space. Quantum mechanics does not admit a completely precise description, in terms of both position and momentum, of an initial condition or "state" (in the classical sense of the word) that would support a precisely deterministic and causal prediction of a final condition.[64][65] In this sense, a quantum phenomenon is a process, a passage from initial to final condition, not an instantaneous "state" in the classical sense of that word.[66][67] Thus there are two kinds of processes in quantum mechanics: stationary and transitional. For a stationary process, the initial and final condition are the same. For a transition, they are different. Obviously by definition, if only the initial condition is given, the process is not determined.[64] Given its initial condition, prediction of its final condition is possible, causally but only probabilistically, because the Schrödinger equation is deterministic for wave function evolution, but the wave function describes the system only probabilistically.[68][69]
For many experiments, it is possible to think of the initial and final conditions of the system as being a particle. In some cases it appears that there are potentially several spatially distinct pathways or trajectories by which a particle might pass from initial to final condition. It is an important feature of the quantum kinematic description that it does not permit a unique definite statement of which of those pathways is actually followed. Only the initial and final conditions are definite, and, as stated in the foregoing paragraph, they are defined only as precisely as allowed by the configuration space description or its equivalent. In every case for which a quantum kinematic description is needed, there is always a compelling reason for this restriction of kinematic precision. An example of such a reason is that for a particle to be experimentally found in a definite position, it must be held motionless; for it to be experimentally found to have a definite momentum, it must have free motion; these two are logically incompatible.[70][71]
Classical kinematics does not primarily demand experimental description of its phenomena. It allows completely precise description of an instantaneous state by a value in phase space, the Cartesian product of configuration and momentum spaces. This description simply assumes or imagines a state as a physically existing entity without concern about its experimental measurability. Such a description of an initial condition, together with Newton's laws of motion, allows a precise deterministic and causal prediction of a final condition, with a definite trajectory of passage.
Relation to general relativity
Even with the defining postulates of both Einstein's theory of general relativity and quantum theory being indisputably supported by rigorous and repeated empirical evidence, and while they do not directly contradict each other theoretically (at least with regard to their primary claims), they have proven extremely difficult to incorporate into one consistent, cohesive model.[73]
Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those particular applications. However, the lack of a correct theory of
Attempts at a unified field theory
The quest to unify the
Another popular theory is
Philosophical implications
Since its inception, the many
The Copenhagen interpretation – due largely to Niels Bohr and Werner Heisenberg – remains most widely accepted some 75 years after its enunciation. According to this interpretation, the probabilistic nature of quantum mechanics is not a temporary feature which will eventually be replaced by a deterministic theory, but is instead a final renunciation of the classical idea of "causality". It also states that any well-defined application of the quantum mechanical formalism must always make reference to the experimental arrangement, due to the conjugate nature of evidence obtained under different experimental situations.
Albert Einstein, himself one of the founders of quantum theory, did not accept some of the more philosophical or metaphysical interpretations of quantum mechanics, such as rejection of
The
In light of the
Applications
Quantum mechanics has had enormous[18] success in explaining many of the features of our universe. Quantum mechanics is often the only theory that can reveal the individual behaviors of the subatomic particles that make up all forms of matter (electrons, protons, neutrons, photons, and others). Quantum mechanics has strongly influenced string theories, candidates for a Theory of Everything (see reductionism).
Quantum mechanics is also critically important for understanding how individual atoms are joined by covalent bonds to form
In many aspects modern technology operates at a scale where quantum effects are significant. Important applications of quantum theory include quantum chemistry, quantum optics, quantum computing, superconducting magnets, light-emitting diodes, the optical amplifier and the laser, the transistor and semiconductors such as the microprocessor, medical and research imaging such as magnetic resonance imaging and electron microscopy.[87] Explanations for many biological and physical phenomena are rooted in the nature of the chemical bond, most notably the macro-molecule DNA.[88]
Electronics
Many modern electronic devices are designed using quantum mechanics. Examples include the
Many electronic devices operate under effect of
Cryptography
Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to more fully develop quantum cryptography, which will theoretically allow guaranteed secure transmission of information.
An inherent advantage yielded by quantum cryptography when compared to classical
Quantum computing
Another goal is the development of
Another active research topic is quantum teleportation, which deals with techniques to transmit quantum information over arbitrary distances.
Macroscale quantum effects
While quantum mechanics primarily applies to the smaller atomic regimes of matter and energy, some systems exhibit quantum mechanical effects on a large scale. Superfluidity, the frictionless flow of a liquid at temperatures near absolute zero, is one well-known example. So is the closely related phenomenon of superconductivity, the frictionless flow of an electron gas in a conducting material (an electric current) at sufficiently low temperatures. The fractional quantum Hall effect is a topological ordered state which corresponds to patterns of long-range quantum entanglement.[91] States with different topological orders (or different patterns of long range entanglements) cannot change into each other without a phase transition.
Quantum theory
Quantum theory also provides accurate descriptions for many previously unexplained phenomena, such as
Examples
Free particle
For example, consider a
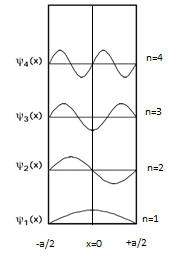
Particle in a box

The particle in a one-dimensional potential energy box is the most mathematically simple example where restraints lead to the quantization of energy levels. The box is defined as having zero potential energy everywhere inside a certain region, and therefore infinite potential energy everywhere outside that region. For the one-dimensional case in the direction, the time-independent Schrödinger equation may be written[96]
With the differential operator defined by
the previous equation is evocative of the classic kinetic energy analogue,
with state in this case having energy coincident with the kinetic energy of the particle.
The general solutions of the Schrödinger equation for the particle in a box are
or, from Euler's formula,
The infinite potential walls of the box determine the values of and at and where must be zero. Thus, at ,
and . At ,
in which cannot be zero as this would conflict with the Born interpretation. Therefore, since , must be an integer multiple of ,
The quantization of energy levels follows from this constraint on since
The ground state energy of the particles is for
The energy of the particle in the th state is
Particle in a box with boundary condition

In this condition the general solution will be same, there will little change to the final result, since the boundary conditions are changed only slightly:
At the wave function is not actually zero at all values of
Clearly, from the wave function variation graph we have, At the wave function follows a cosine curve with as the origin.
At the wave function follows a sine curve with as the origin.
From this observation we can conclude that the wave function is alternatively sine and cosine. So in this case the resultant wave equation is
Finite potential well
A finite potential well is the generalization of the infinite potential well problem to potential wells having finite depth.
The finite potential well problem is mathematically more complicated than the infinite particle-in-a-box problem as the wave function is not pinned to zero at the walls of the well. Instead, the wave function must satisfy more complicated mathematical boundary conditions as it is nonzero in regions outside the well.
Rectangular potential barrier
This is a model for the
Harmonic oscillator
As in the classical case, the potential for the quantum harmonic oscillator is given by
This problem can either be treated by directly solving the Schrödinger equation, which is not trivial, or by using the more elegant "ladder method" first proposed by Paul Dirac. The
where Hn are the Hermite polynomials
and the corresponding energy levels are
This is another example illustrating the quantification of energy for bound states.
Step potential

The potential in this case is given by:
The solutions are superpositions of left- and right-moving waves:
and
- ,
with coefficients A and B determined from the
and
- .
Each term of the solution can be interpreted as an incident, reflected, or transmitted component of the wave, allowing the calculation of transmission and reflection coefficients. Notably, in contrast to classical mechanics, incident particles with energies greater than the potential step are partially reflected.
See also
- Angular momentum diagrams (quantum mechanics)
- Einstein's thought experiments
- Hamiltonian (quantum mechanics)
- Two-state quantum system
- Fractional quantum mechanics
- List of quantum-mechanical systems with analytical solutions
- List of textbooks on classical and quantum mechanics
- Macroscopic quantum phenomena
- Phase space formulation
- Regularization (physics)
- Spherical basis
Notes
- )
- ISBN 978-0201500646. Archived from the originalon 2018-11-26. Retrieved 2017-01-03.
- .
- ISBN 0-521-49730-2
- ^ Max Born & Emil Wolf, Principles of Optics, 1999, Cambridge University Press
- ^ "Thomas Young's experiment". www.cavendishscience.org. Retrieved 2017-07-23.
- ISBN 978-0387906423.
- ^ Stachel, John (2009) “Bohr and the Photon” Quantum Reality, Relativistic Causality and the Closing of the Epistemically Circle. Dordrecht, Springer p. 79.
- .
- ISBN 978-0195023831.
- ^ Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com
- . Reprinted in The collected papers of Albert Einstein, John Stachel, editor, Princeton University Press, 1989, Vol. 2, pp. 149–166, in German; see also Einstein's early work on the quantum hypothesis, ibid. pp. 134–148.
- ISBN 9780080121024
- ISBN 978-1-57955-008-0.
- )
- ^ a b c See, for example, the Feynman Lectures on Physics for some of the technological applications which use quantum mechanics, e.g., transistors (vol III, pp. 14–11 ff), integrated circuits, which are follow-on technology in solid-state physics (vol II, pp. 8–6), and lasers (vol III, pp. 9–13).
- .
- ^ a b A New Kind of Science Note (a) for Quantum phenomena
- ^ Feynman, Richard. "The Feynman Lectures on Physics III 21-4". California Institute of Technology. Retrieved 2015-11-24.
"...it was long believed that the wave function of the Schrödinger equation would never have a macroscopic representation analogous to the macroscopic representation of the amplitude for photons. On the other hand, it is now realized that the phenomena of superconductivity presents us with just this situation.
- ^ Richard Packard (2006) "Berkeley Experiments on Superfluid Macroscopic Quantum Effects" Archived November 25, 2015, at the Wayback Machine accessdate=2015-11-24
- ^ "Quantum – Definition and More from the Free Merriam-Webster Dictionary". Merriam-webster.com. Retrieved 2012-08-18.
- ^ Thall, Edwin. "Thall's History of Quantum Mechanics". Florida Community College at Jacksonville. Archived from the original on October 7, 2009. Retrieved May 23, 2009.
- ^ "ysfine.com". Retrieved 11 September 2015.
- geocities.com. 2009-10-26. Archived from the originalon 2009-10-26. Retrieved 2016-06-13.
- ^ P.A.M. Dirac, The Principles of Quantum Mechanics, Clarendon Press, Oxford, 1930.
- ^ D. Hilbert Lectures on Quantum Theory, 1915–1927
- ^ J. von Neumann, Mathematische Grundlagen der Quantenmechanik, Springer, Berlin, 1932 (English translation: Mathematical Foundations of Quantum Mechanics, Princeton University Press, 1955).
- ^ H.Weyl "The Theory of Groups and Quantum Mechanics", 1931 (original title: "Gruppentheorie und Quantenmechanik").
- Dirac, P.A.M.(1958). The Principles of Quantum Mechanics, 4th edition, Oxford University Press, Oxford, p. ix: "For this reason I have chosen the symbolic method, introducing the representatives later merely as an aid to practical calculation."
- ^ "Heisenberg – Quantum Mechanics, 1925–1927: The Uncertainty Relations". Aip.org. Retrieved 2012-08-18.
- ^
- ^ Lodha, Suresh K.; Faaland, Nikolai M.; et al. (2002). "Visualization of Uncertain Particle Movement (Proceeding Computer Graphics and Imaging)" (PDF). Actapress.com. Archived (PDF) from the original on 2018-08-01. Retrieved 2018-08-01.
- ISBN 978-0-521-80412-7., Chapter, p.
- ^ "dict.cc dictionary :: eigen :: German-English translation". dict.cc. Retrieved 11 September 2015.
- ^ "Topics: Wave-Function Collapse". Phy.olemiss.edu. 2012-07-27. Archived from the original on 2017-02-28. Retrieved 2012-08-18.
- ^ "Collapse of the wave-function". Farside.ph.utexas.edu. Retrieved 2012-08-18.
- ^ Michael Trott. "Time-Evolution of a Wavepacket in a Square Well – Wolfram Demonstrations Project". Demonstrations.wolfram.com. Retrieved 2010-10-15.
- ^ Michael Trott. "Time Evolution of a Wavepacket In a Square Well". Demonstrations.wolfram.com. Retrieved 2010-10-15.
- ^ "Wave Functions and the Schrödinger Equation" (PDF). Retrieved 2010-10-15.[dead link]
- Acta Physica Polonica B. 19 (8): 683–695. Retrieved 13 June 2016.
- ^ Nancy Thorndike Greenspan, "The End of the Certain World: The Life and Science of Max Born" (Basic Books, 2005), pp. 124–128, 285–826.
- ^ "Archived copy" (PDF). Archived from the original (PDF) on 2011-07-19. Retrieved 2009-06-04.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ "The Nobel Prize in Physics 1979". Nobel Foundation. Retrieved 2010-02-16.
- ].
- ^ See, for example, Precision tests of QED. The relativistic refinement of quantum mechanics known as quantum electrodynamics (QED) has been shown to agree with experiment to within 1 part in 108 for some atomic properties.
- ISBN 978-0-7167-7550-8.
- .
- ISBN 978-9810204754.
- .
- ^ N.P. Landsman (June 13, 2005). "Between classical and quantum" (PDF). Retrieved 2012-08-19. Handbook of the Philosophy of Science Vol. 2: Philosophy of Physics (eds. John Earman & Jeremy Butterfield).
- ^ (see macroscopic quantum phenomena, Bose–Einstein condensate, and Quantum machine)
- ^ "Atomic Properties". Academic.brooklyn.cuny.edu. Retrieved 2012-08-18.
- ^ http://assets.cambridge.org/97805218/29526/excerpt/9780521829526_excerpt.pdf
- ^ Born, M., Heisenberg, W., Jordan, P. (1926). Z. Phys. 35: 557–615. Translated as 'On quantum mechanics II', pp. 321–385 in Van der Waerden, B.L. (1967), Sources of Quantum Mechanics, North-Holland, Amsterdam, "The basic difference between the theory proposed here and that used hitherto ... lies in the characteristic kinematics ...", p. 385.
- ^ Dirac, P.A.M. (1930/1958). The Principles of Quantum Mechanics, fourth edition, Oxford University Press, Oxford UK, p. 5: "A question about what will happen to a particular photon under certain conditions is not really very precise. To make it precise one must imagine some experiment performed having a bearing on the question, and enquire what will be the result of the experiment. Only questions about the results of experiments have a real significance and it is only such questions that theoretical physics has to consider."
- ISBN 0-444-89892-1, pp. 303–322. "The essential lesson of the analysis of measurements in quantum theory is thus the emphasis on the necessity, in the account of the phenomena, of taking the whole experimental arrangement into consideration, in complete conformity with the fact that all unambiguous interpretation of the quantum mechanical formalism involves the fixation of the external conditions, defining the initial state of the atomic system and the character of the possible predictions as regards subsequent observable properties of that system. Any measurement in quantum theory can in fact only refer either to a fixation of the initial state or to the test of such predictions, and it is first the combination of both kinds which constitutes a well-defined phenomenon."
- ^ Bohr, N. (1948). On the notions of complementarity and causality, Dialectica 2: 312–319. "As a more appropriate way of expression, one may advocate limitation of the use of the word phenomenon to refer to observations obtained under specified circumstances, including an account of the whole experiment."
- ISBN 978-3-642-71899-1, Chapter XIII, Special Structures in Preparation and Registration Devices, §1, Measurement chains, p. 132.
- ^ a b Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Z. Phys. 43: 172–198. Translation as 'The actual content of quantum theoretical kinematics and mechanics' here [1], "But in the rigorous formulation of the law of causality, – "If we know the present precisely, we can calculate the future" – it is not the conclusion that is faulty, but the premise."
- ^ Green, H.S. (1965). Matrix Mechanics, with a foreword by Max Born, P. Noordhoff Ltd, Groningen. "It is not possible, therefore, to provide 'initial conditions' for the prediction of the behaviour of atomic systems, in the way contemplated by classical physics. This is accepted by quantum theory, not merely as an experimental difficulty, but as a fundamental law of nature", p. 32.
- ^ Rosenfeld, L. (1957). Misunderstandings about the foundations of quantum theory, pp. 41–45 in Observation and Interpretation, edited by S. Körner, Butterworths, London. "A phenomenon is therefore a process (endowed with the characteristic quantal wholeness) involving a definite type of interaction between the system and the apparatus."
- ISBN 90-277-0345-0, p. 5: "That led Heisenberg to his really masterful step forward, resulting in the new quantum mechanics. His idea was to build up a theory entirely in terms of quantities referring to two states."
- ^ Born, M. (1927). Physical aspects of quantum mechanics, Nature 119: 354–357, "These probabilities are thus dynamically determined. But what the system actually does is not determined ..."
- ^ Messiah, A. (1961). Quantum Mechanics, volume 1, translated by G.M. Temmer from the French Mécanique Quantique, North-Holland, Amsterdam, p. 157.
- doi:10.1038/121580a0.
- ^ Heisenberg, W. (1930). The Physical Principles of the Quantum Theory, translated by C. Eckart and F.C. Hoyt, University of Chicago Press.
- ISBN 0-201-02510-8.
- ISBN 0-08-016025-5
- ^ "Stephen Hawking; Gödel and the end of physics". cam.ac.uk. Archived from the original on 21 May 2011. Retrieved 11 September 2015.
- ISBN 978-1400834747.
- ^
Tatsumi Aoyama; Masashi Hayakawa; Toichiro Kinoshita; Makiko Nio (2012). "Tenth-Order QED Contribution to the Electron g-2 and an Improved Value of the Fine Structure Constant". PMID 23005618.
- ^ Parker, B. (1993). Overcoming some of the problems. pp. 259–279.
- ^ The Character of Physical Law (1965) Ch. 6; also quoted in The New Quantum Universe (2003), by Tony Hey and Patrick Walters
- .
- ISBN 978-0-521-66148-5.
- ^ "Action at a Distance in Quantum Mechanics (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. 2007-01-26. Retrieved 2012-08-18.
- ISBN 978-1-57955-008-0.
- ^ "Everett's Relative-State Formulation of Quantum Mechanics (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. Retrieved 2012-08-18.
- .
- ISBN 978-0-521-76415-5. p. 35.
- ISBN 9780486648712. Retrieved 2012-08-18.
- ^ Matson, John. "What Is Quantum Mechanics Good for?". Scientific American. Retrieved 18 May 2016.
- ^ The Nobel laureates Watson and Crick cited Pauling, Linus (1939). The Nature of the Chemical Bond and the Structure of Molecules and Crystals. Cornell University Press. for chemical bond lengths, angles, and orientations.
- ISBN 978-0471117094.
- ^ "Applications of Quantum Computing". research.ibm.com. Retrieved 28 June 2017.
- .
- ^ Anderson, Mark (2009-01-13). "Is Quantum Mechanics Controlling Your Thoughts? | Subatomic Particles". Discover Magazine. Retrieved 2012-08-18.
- ^ "Quantum mechanics boosts photosynthesis". physicsworld.com. Retrieved 2010-10-23.
- Chapter 6, p. 79
- ISBN 9789812708991. Retrieved 2012-08-18.
- ^ Derivation of particle in a box, chemistry.tidalswan.com
- ^ N.B. on precision: If and are the precisions of position and momentum obtained in an individual measurement and , their standard deviations in an ensemble of individual measurements on similarly prepared systems, then "There are, in principle, no restrictions on the precisions of individual measurements and , but the standard deviations will always satisfy ".[4]
References
The following titles, all by working physicists, attempt to communicate quantum theory to lay people, using a minimum of technical apparatus.
- Chester, Marvin (1987) Primer of Quantum Mechanics. John Wiley. ISBN 0-486-42878-8
- ISBN 978-1-84614-432-5.
- , yet containing many insights for the expert.
- Ghirardi, GianCarlo, 2004. Sneaking a Look at God's Cards, Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using algebra, trigonometry, and bra–ket notation can be passed over on a first reading.
- N. David Mermin, 1990, "Spooky actions at a distance: mysteries of the QT" in his Boojums all the way through. Cambridge University Press: 110–76.
- philosophicalconsiderations.
More technical:
- ISBN 0-691-08131-X
- ISBN 978-0-19-852011-5. The beginning chapters make up a very clear and comprehensible introduction.
- .
- ISBN 978-0-7382-0008-8.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. OCLC 40251748. A standard undergraduate text.
- Max Jammer, 1966. The Conceptual Development of Quantum Mechanics. McGraw Hill.
- Hagen Kleinert, 2004. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 3rd ed. Singapore: World Scientific. Draft of 4th edition.
- Gunther Ludwig, 1968. Wave Mechanics. London: Pergamon Press. ISBN 0-08-203204-1
- ISBN 0-486-43517-2.
- Albert Messiah, 1966. Quantum Mechanics (Vol. I), English translation from French by G.M. Temmer. North Holland, John Wiley & Sons. Cf. chpt. IV, section III. online
- OCLC 39849482.
- Scerri, Eric R., 2006. The ISBN 0-19-530573-6
- OCLC 34661512.
- ISBN 978-0-691-02893-4.
- Hermann Weyl, 1950. The Theory of Groups and Quantum Mechanics, Dover Publications.
- D. Greenberger, K. Hentschel, F. Weinert, eds., 2009. Compendium of quantum physics, Concepts, experiments, history and philosophy, Springer-Verlag, Berlin, Heidelberg.
Further reading
- Bernstein, Jeremy (2009). Quantum Leaps. Cambridge, Massachusetts: Belknap Press of Harvard University Press. ISBN 978-0-674-03541-6.
- ISBN 978-0-486-65969-5.
- Eisberg, Robert; ISBN 978-0-471-87373-0.
- ISBN 978-0-8053-8714-8.
- Merzbacher, Eugen (1998). Quantum Mechanics. Wiley, John & Sons, Inc. ISBN 978-0-471-88702-7.
- ISBN 978-0-201-53929-5.
- Shankar, R. (1994). Principles of Quantum Mechanics. Springer. ISBN 978-0-306-44790-7.
- Stone, A. Douglas (2013). Einstein and the Quantum. Princeton University Press. ISBN 978-0-691-13968-5.
- Veltman, Martinus J.G. (2003), Facts and Mysteries in Elementary Particle Physics.
- Zucav, Gary (1979, 2001). The Dancing Wu Li Masters: An overview of the new physics (Perennial Classics Edition) HarperCollins.
On Wikibooks
External links
- 3D animations, applications and research for basic quantum effects (animations also available in commons.wikimedia.org (Université paris Sud))
- Quantum Cook Book by R. Shankar, Open Yale PHYS 201 material (4pp)
- The Modern Revolution in Physics – an online textbook.
- J. O'Connor and E.F. Robertson: A history of quantum mechanics.
- Introduction to Quantum Theory at Quantiki.
- Quantum Physics Made Relatively Simple: three video lectures by Hans Bethe
- H is for h-bar.
- Quantum Mechanics Books Collection: Collection of free books
- Course material
- A collection of lectures on Quantum Mechanics
- Quantum Physics Database – Fundamentals and Historical Background of Quantum Theory.
- Doron Cohen: Lecture notes in Quantum Mechanics (comprehensive, with advanced topics).
- MIT OpenCourseWare: Chemistry.
- MIT OpenCourseWare: Physics. See 8.04
- Stanford Continuing Education PHY 25: Quantum Mechanics by Leonard Susskind, see course description[permanent dead link] Fall 2007
- 5½ Examples in Quantum Mechanics
- Imperial College Quantum Mechanics Course.
- Spark Notes – Quantum Physics.
- Quantum Physics Online : interactive introduction to quantum mechanics (RS applets).
- Experiments to the foundations of quantum physics with single photons.
- AQME : Advancing Quantum Mechanics for Engineers – by T. Barzso, D. Vasileska and G. Klimeck online learning resource with simulation tools on nanohub
- Quantum Mechanics by Martin Plenio
- Quantum Mechanics by Richard Fitzpatrick
- Online course on Quantum Transport
- FAQs
- Media
- PHYS 201: Fundamentals of Physics II by Ramamurti Shankar, Open Yale Course
- Lectures on Quantum Mechanics by Leonard Susskind
- Everything you wanted to know about the quantum world – archive of articles from New Scientist.
- Quantum Physics Research from Science Daily
- Overbye, Dennis (December 27, 2005). "Quantum Trickery: Testing Einstein's Strangest Theory". The New York Times. Retrieved April 12, 2010.
- Audio: Astronomy Cast Quantum Mechanics – June 2009. Fraser Cain interviews Pamela L. Gay.
- "The Physics of Reality", BBC Radio 4 discussion with Roger Penrose, Fay Dowker & Tony Sudbery (In Our Time, May 2, 2002).
- Philosophy
- Ismael, Jenann. "Quantum Mechanics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- Krips, Henry. "Measurement in Quantum Theory". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.





















































